【题目】用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论并证明你的结论;
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?简要说明理由.

参考答案:
【答案】(1)BE=CF.见解析;(2)BE=CF仍然成立.理由见解析.
【解析】
(1)根据图形中BE、CF的长度可以直接得出BE=CF的结论,当然也可以通过证明△ABE≌△ACF得出结论.
(2)可以通过证明△ADF≌△ACE,得出CE=DF,进而得出BE=CF.
(1)BE=CF.
证明:在△ABE和△ACF中,
∵∠BAE+∠EAC=∠CAF+∠EAC=60°,
∴∠BAE=∠CAF.
∵AB=AC,∠B=∠ACF=60°,∴△ABE≌△ACF(ASA).
∴BE=CF;
(2)BE=CF仍然成立.
证明:在△ACE和△ADF中,
∵∠CAE+∠EAD=∠FAD+∠DAE=60°,
∴∠CAE=∠DAF,
∵∠BCA=∠ACD=60°,
∴∠FCE=60°,
∴∠ACE=120°,
∵∠ADC=60°,
∴∠ADF=120°,
在△ACE和△ADF中,

∴△ADF≌△ACE,
∴CE=DF,
∴BE=CF.
-
科目: 来源: 题型:
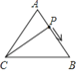
查看答案和解析>>【题目】如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,
 ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=
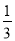 ,求DE的长.
,求DE的长.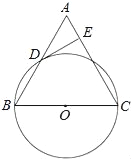
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段

求作:菱形
 ,使得
,使得 且
且 .
.以下是小丁同学的作法:
①作线段
 ;
;②分别以点
 ,
, 为圆心,线段
为圆心,线段 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点 ;
;③再分别以点
 ,
, 为圆心,线段
为圆心,线段 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点 ;
;④连接
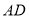 ,
, ,
, .
.则四边形
 即为所求作的菱形.(如图)
即为所求作的菱形.(如图)老师说小丁同学的作图正确.则小丁同学的作图依据是:_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠D应分别是20°和30°.
(1)李叔叔量得∠BCD=142°,根据李叔叔量得的结果,你能断定这个零件是否合格?请解释你的结论.
(2)你知道∠B、∠D、∠BCD三角之间有何关系吗?请写出你的结论(不需说明理由).

相关试题

