【题目】如图,直线 m,n 相交于 O,所夹的锐角是 53°,点 P,Q 分别是直线 m,n上的点,将直线 m,n 按照下面的程序操作,能使两直线平行的是( )

A. 将直线 m 以点 O 为中心,顺时针旋转 53° B. 将直线 n 以点 Q 为中心,顺时针旋转 53°
C. 将直线 m 以点 P 为中心,顺时针旋转 53° D. 将直线 m 以点 P 为中心,顺时针旋转 127°
参考答案:
【答案】C
【解析】
根据平行判定定理和性质一一判定即可求解.
将直线 m 以点 O 为中心,顺时针旋转 53°,有交点不平行,故错误.
将直线 n 以点 Q 为中心,顺时针旋转 53°,有交点不平行,故错误.
将直线 m 以点 P 为中心,顺时针旋转 53°,平行,正确.
将直线 m 以点 P 为中心,顺时针旋转 127°,同位角不相等不平行,故错误.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为12 ,点B在点A右边,且OA2OB.
(1)写出数轴上点 B 表示的数;
(2)点 M 为数轴上一点,若 AM BM 4 ,求出点 M 表示的数.

-
科目: 来源: 题型:
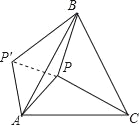
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人.
(1)求第一轮后患病的人数;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个动点P在平面直角坐标系中按箭头所示方向作折线运动,即第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),……,按这样的运动规律,经过第2019次运动后,动点P的坐标是___________
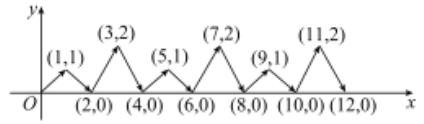
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.
 ;
;  ;
;  ;
;(3)求出△ABC的面积
相关试题

