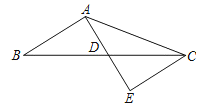
【题目】如图,在△ABC中,AB=3,AC=5,AD是BC边上的中线,且AD=2,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用全等三角形的性质证明AB=EC=3,再利用勾股定理逆定理判断即可.
(2)解直角三角形求出CD即可解决问题.
(1)证明:
∵AD是BC边上的中线
∴BD=CD
又∵DE=AD,∠ADB=∠CDE
∴△ABD≌△ECD(SAS),
∴EC=AB=3,
∵AE=4,AC=5
∴△AEC 中,AE2+EC2=AC2
∴△AEC是直角三角形.
(2)解:在Rt△CDE中,CD2=CE2+DE2=32+22=13
∴CD=![]()
∴BC=2CD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形A1B1C1O、A2B2C2C1……按照如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),B3(7,4),则B2019的坐标是_____.

-
科目: 来源: 题型:
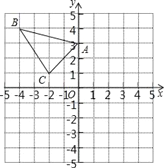
查看答案和解析>>【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店计划购进A、B两种型号的电动自行车共30辆,其中A型电动自行车不少于20辆,A、B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.
(1)求出y与m之间的函数关系式;
(2)该商店如何进货才能获得最大利润?此时最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:
(1)求直线AC的解析式;
(2)求△OAC的面积;
(3)是否存在点M、使△OMC的面积是△OAC的面积的
 ?若存在,求出此时点M的坐标;若不存在,请说明理由?
?若存在,求出此时点M的坐标;若不存在,请说明理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线PT与⊙O相交于点T,直线PO与⊙O相交于A,B两点.已知∠PTA=∠B.
(1)求证:PT是⊙O的切线;
(2)若PT=6,PA=4,求⊙O的半径;
(3)若PT=TB=
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是 ( )

A.8+2aB.8aC.6+aD.6+2a
相关试题

