【题目】如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P,Q,R分别在AB,BC,CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,在运动过程中:
(1)求证:△APR,△BPQ,△CQR的面积相等;
(2)求△PQR面积的最小值;
(3)用t(秒)(0≤t≤2)表示运动时间,是否存在t,使∠PQR=90°?若存在,请直接写出t的值;若不存在,请说明理由.

参考答案:
【答案】(1)证明见解析;(2)6;(3)t=1或![]() .
.
【解析】试题分析:(1)先利用锐角三角函数表示出QE=4t,QD=3(2﹣t),再由运动得出AP=3t,CR=4t,BP=3(2﹣t),AR=4(2﹣t),最后用三角形的面积公式即可得出结论;
(2)借助(1)得出的结论,利用面积差得出S△PQR=18(t﹣1)2+6,即可得出结论;
(3)先判断出∠DQR=∠EQP,用此两角的正切值建立方程求解即可.
试题解析:解:(1)如图,在Rt△ABC中,AB=6,AC=8,根据勾股定理得,BC=10,sin∠B=![]() =
=![]() =
=![]() ,sin∠C=
,sin∠C=![]() ,过点Q作QE⊥AB于E,在Rt△BQE中,BQ=5t,∴sin∠B=
,过点Q作QE⊥AB于E,在Rt△BQE中,BQ=5t,∴sin∠B=![]() =
=![]() ,∴QE=4t,过点Q作QD⊥AC于D,在Rt△CDQ中,CQ=BC﹣BQ=10﹣5t,∴QD=CQsin∠C=
,∴QE=4t,过点Q作QD⊥AC于D,在Rt△CDQ中,CQ=BC﹣BQ=10﹣5t,∴QD=CQsin∠C=![]() (10﹣5t)=3(2﹣t),由运动知,AP=3t,CR=4t,∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),∴S△APR=
(10﹣5t)=3(2﹣t),由运动知,AP=3t,CR=4t,∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),∴S△APR=![]() APAR=
APAR=![]() ×3t×4(2﹣t)=6t(2﹣t),S△BPQ=
×3t×4(2﹣t)=6t(2﹣t),S△BPQ=![]() BPQE=
BPQE=![]() ×3(2﹣t)×4t=6t(2﹣t),S△CQR=
×3(2﹣t)×4t=6t(2﹣t),S△CQR=![]() CRQD=
CRQD=![]() ×4t×3(2﹣t)=6t(2﹣t),∴S△APR=S△BPQ=S△CQR,∴△APR,△BPQ,△CQR的面积相等;
×4t×3(2﹣t)=6t(2﹣t),∴S△APR=S△BPQ=S△CQR,∴△APR,△BPQ,△CQR的面积相等;

(2)由(1)知,S△APR=S△BPQ=S△CQR=6t2﹣t),∵AB=6,AC=8,∴S△PQR=S△ABC﹣(S△APR+S△BPQ+S△CQR)
=![]() ×6×8﹣3×6t(2﹣t)=24﹣18(2t﹣t2)=18(t﹣1)2+6,∵0≤t≤2,∴当t=1时,S△PQR最小=6;
×6×8﹣3×6t(2﹣t)=24﹣18(2t﹣t2)=18(t﹣1)2+6,∵0≤t≤2,∴当t=1时,S△PQR最小=6;
(3)存在,由点P,Q,R的运动速度知,运动1秒时,点P,Q,R分别在AB,BC,AC的中点,此时,四边形APQR是矩形,即:t=1秒时,∠PQR=90°,由(1)知,QE=4t,QD=3(2﹣t),AP=3t,CR=4t,AR=4(2﹣t),∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),过点Q作QD⊥AC于D,作QE⊥AB于E,∵∠A=90°,∴四边形APQD是矩形,∴AE=DQ=3(2﹣t),AD=QE=4t,∴DR=|AD﹣AR|=|4t﹣4(2﹣t)|=4|2t﹣2|,PE=|AP﹣AE|=|3t﹣3(2﹣t)|=3|2t﹣2|.∵∠DQE=90°,∠PQR=90°,∴∠DQR=∠EQP,∴tan∠DQR=tan∠EQP,在Rt△DQR中,tan∠DQR=![]() =
=![]() ,在Rt△EQP中,tan∠EQP=
,在Rt△EQP中,tan∠EQP=![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴16t=9(2﹣t),∴t=
,∴16t=9(2﹣t),∴t=![]() .即:t=1或
.即:t=1或![]() 秒时,∠PQR=90°.
秒时,∠PQR=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2018的相反数是_____,单项式﹣3x2yz3的系数是_____,次数是_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,﹣2),请你帮她画出坐标系,并写出其他各景点的坐标.
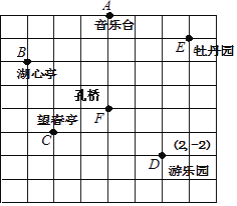
-
科目: 来源: 题型:
查看答案和解析>>【题目】按“有无曲面”将下列几何体分类则与其他三个几何体不相同的一个是( )
A.圆柱B.圆锥C.球D.立方体
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线 l上,边EF与边AC重合,且EF=FP.
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,
BQ.猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;
(3)AP,BQ .你认为(2)中所猜想的BQ 与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
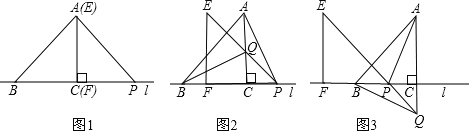
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、B、F、C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )

A. AB=DE B. DF∥AC C. ∠E=∠ABC D. AB∥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
相关试题

