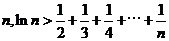(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数 的分布列及期望
的分布列及期望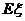 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
- 答案
一.1-5 ACDAD 6-10 DBDAB 11-12 BA
13. 28 14. 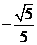 15. 1 16. ⑴⑵⑷
15. 1 16. ⑴⑵⑷
17. 解:(1)∵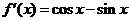 ,……………………………………………(2分)
,……………………………………………(2分)
∴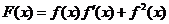
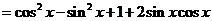
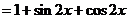
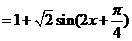 ……………(3分)
……………(3分)
∴当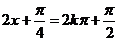
 (
( )时,
)时,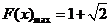
最小正周期为 ……………………………………………(5分)
……………………………………………(5分)
(2)∵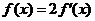
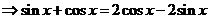
∴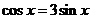
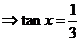 ……………………………………………(8分)
……………………………………………(8分)
∴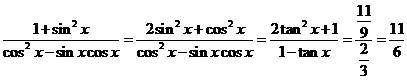 …………(10分)
…………(10分)
18.解法一:证明:连结OC,
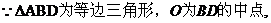
∴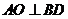 . ----------------------------------------------------------------------------------1分
. ----------------------------------------------------------------------------------1分
 ,
, ,
,
∴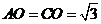 .
------------------------------------------------------2分
.
------------------------------------------------------2分
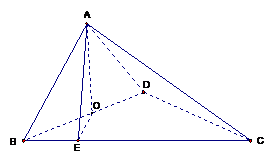 在
在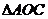 中,
中,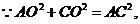
∴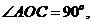 即
即 ------------------3分
------------------3分
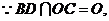
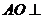 面
面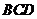 . ----------------------------4分
. ----------------------------4分
(II)过O作 ,连结AE,
,连结AE,
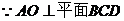 ,
,
∴AE在平面BCD上的射影为OE.
∴ .
.
∴ 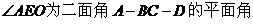 .
-----------------------------------------7分
.
-----------------------------------------7分
在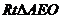 中,
中,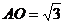 ,
,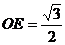 ,
,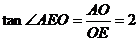 ,
,
∴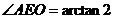 .∴二面角A-BC-D的大小为
.∴二面角A-BC-D的大小为 . -------8分
. -------8分
(III)解:设点O到平面ACD的距离为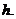
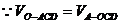 ,
,
∴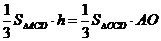 .
.
在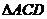 中,
中, ,
,
 .
.
而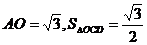 ,∴
,∴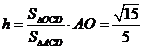 .
.
∴点O到平面ACD的距离为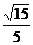 .-----------------------------------------------------12分
.-----------------------------------------------------12分
解法二:(I)同解法一.(II)解:以O为原点,如图建立空间直角坐标系,
 则
则 
 ,
,
∴ . ------------6分
. ------------6分
设平面ABC的法向量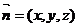 ,
,
 ,
,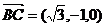 ,
,
由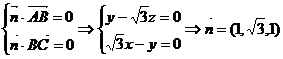 .
.
设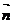 与
与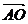 夹角为
夹角为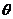 ,则
,则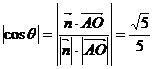 .
.
∴二面角A-BC-D的大小为 .
--------------------8分
.
--------------------8分
(III)解:设平面ACD的法向量为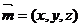 ,又
,又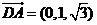 ,
,
 .
-----------------------------------11分
.
-----------------------------------11分
设 与
与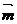 夹角为
夹角为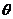 ,
,
则  - 设O 到平面ACD的距离为h,
- 设O 到平面ACD的距离为h,
∵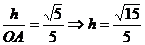 ,∴O到平面ACD的距离为
,∴O到平面ACD的距离为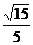 . ---------------------12分
. ---------------------12分
19.解:(Ⅰ)记“厂家任取4件产品检验,其中至少有1件是合格品”为事件A
用对立事件A来算,有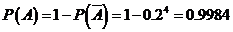 ………3分
………3分
(Ⅱ) 可能的取值为
可能的取值为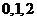
 ,
, ,
,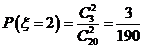 ………
………

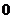
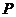
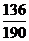
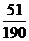
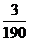
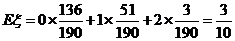 ………………9分
………………9分
记“商家任取2件产品检验,都合格”为事件B,则商家拒收这批产品的概率
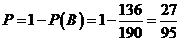 所以商家拒收这批产品的概率为
所以商家拒收这批产品的概率为 ………………….12分
………………….12分
20. (1)当 (1分)
(1分)
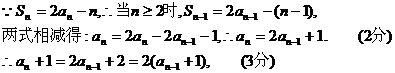
 为首项,2为公比的等比例数列。(6分)
为首项,2为公比的等比例数列。(6分)
(2)得 (7分)
(7分)
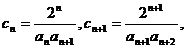
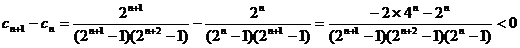
 。(11分)
。(11分)
 12分
12分
21解(I)设
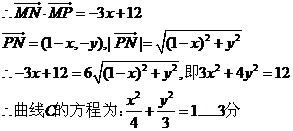
(Ⅱ)(1)当直线 的斜率不存在时,方程为
的斜率不存在时,方程为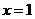
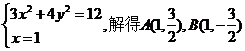
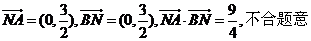 …………(4分)
…………(4分)
(2)当直线 的斜率存在时,设直线的方程为
的斜率存在时,设直线的方程为 ,
,
设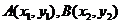 ,
,
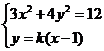 ,得
,得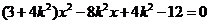
 …………(6分)
…………(6分)

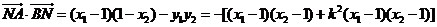
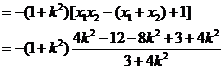
 …………………8分
…………………8分
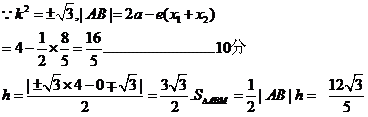
注意也可用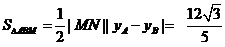 ..........12分
..........12分
22.  解:(1)因为
解:(1)因为 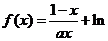 所以
所以

 依题意可得,对
依题意可得,对 恒成立,
恒成立,

 所以 对
所以 对 恒成立,
恒成立,

 所以 对
所以 对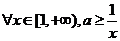 恒成立,
恒成立,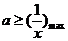 ,即
,即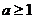

 (2)当
(2)当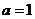 时,
时,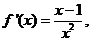 若
若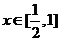 ,
, ,
,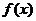 单调递减;
单调递减;

 若
若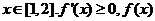 单调递增;
单调递增;

 故
故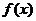 在
在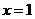 处取得极小值,即最小值
处取得极小值,即最小值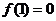

 又
又


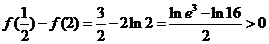

 所以要使直线
所以要使直线 与函数
与函数 的图象在
的图象在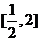 上有两个不同交点,
上有两个不同交点,

 实数
实数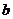 的取值范围应为
的取值范围应为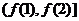 ,即(
,即(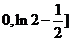 ;
;

 (3)当
(3)当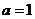 时,由
时,由 可知,
可知, 在
在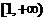 上为增函数,
上为增函数,

 当
当 时,令
时,令 ,则
,则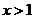 ,故
,故 ,
,


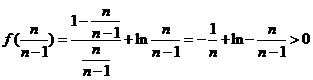 所以
所以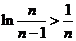 。
。

 故
故 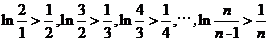

 相加可得
相加可得

 又因为
又因为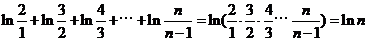

 所以对大于1的任意正整书
所以对大于1的任意正整书