【解析】（1）证明：对y = x2
+ 2求导得：y′= 2x，则y′
即l1，l2的斜率分别为2x1，2x2．又由
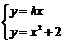得x2 ? kx + 2 = 0 ①
∴x1 + x2 = k即2x1 + 2x2 = 2k．∴2x1，k，2x2成等差数列．
- 答案
搜索
【解析】（1）证明：对y = x2
+ 2求导得：y′= 2x，则y′即l1，l2的斜率分别为2x1，2x2．又由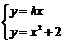得x2 ? kx + 2 = 0 ①
∴x1 + x2 = k即2x1 + 2x2 = 2k．∴2x1，k，2x2成等差数列．
