一、选择题:
题 号
1
2
3
4
5
6
7
8
9
10
11
12
答 案
B
A
D
B
D
B
C
C
A
B
D
A
二、填空题:
13.1 14.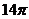 15.5 16.
15.5 16.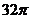
三、解答题:
17.解:(I)设“甲射击5次,有两次未击中目标”为事件A,则
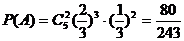
答:甲射击5次,有两次未击中目标的概率为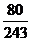
 …………5分
…………5分
(Ⅱ)设“两人各射击4次,甲恰好击中目标2次,且乙恰好击中目标3次”为事件B,则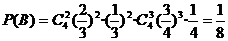
答:两人各射击4次,甲恰好击中目标2次,且乙恰好击中目标3次的概率为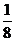

………………10分
18.解:(I)
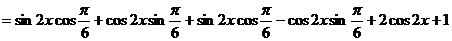 ……2分
……2分

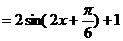 ………………………………………4分
………………………………………4分
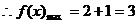
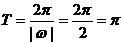 ………………………………………6分
………………………………………6分
(II)由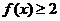
得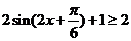
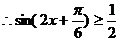
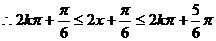
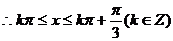
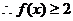 的x的取值范围是
的x的取值范围是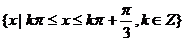 …………12分
…………12分
19.解:(Ⅰ)因为四棱锥P―ABCD的底面是正方形,PA⊥底面ABCD,
则CD⊥侧面PAD
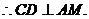
又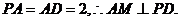
又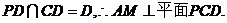 ……………5分
……………5分
(Ⅱ)建立如图所示的空间直角坐标系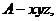 又PA=AD=2,
又PA=AD=2,
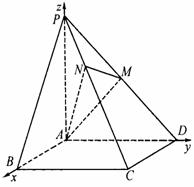

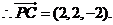
设 则有 则有 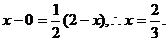
同理可得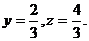 即得 …………………………8分 …………………………8分 由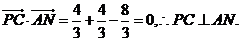 
而平面PAB的法向量可为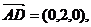 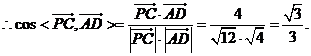
故所求平面AMN与PAB所成锐二面角的大小为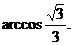 …………12分 …………12分 20.解:(Ⅰ)∵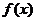 为奇函数, 为奇函数, ∴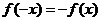 即 ∴ ………………………………………2分 ………………………………………2分 ∵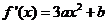 的最小值为 的最小值为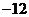 ∴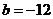 又直线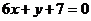 的斜率为 的斜率为 因此,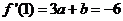 ∴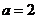 , ,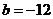 , ,  ………………………………………5分 ………………………………………5分 (Ⅱ)由(Ⅰ)知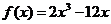  ∴ ,列表如下: ,列表如下: 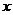
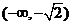

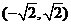
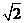

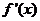
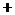

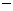

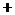
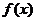
极大 
极小 
所以函数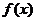 的单调增区间是 的单调增区间是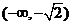 和 和 …………8分 …………8分 ∵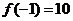 , ,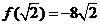 , ,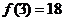 ∴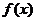 在 在 上的最大值是 上的最大值是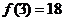 ,最小值是 ,最小值是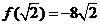 ………12分 ………12分 21.解:(Ⅰ)设d、q分别为数列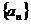 、数列 、数列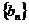 的公差与公比. 的公差与公比. 由题可知, 分别加上1,1,3后得2,2+d,4+2d 分别加上1,1,3后得2,2+d,4+2d 是等比数列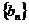 的前三项, 的前三项, 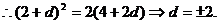
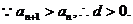
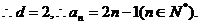 ……………4分 ……………4分
由此可得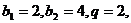 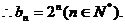 …………………………6分 …………………………6分
(Ⅱ)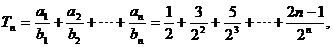 ① ① 当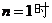 , , 当 , ,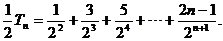 ② ② ①―②,得 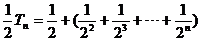 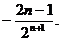
 ………………9分 ………………9分
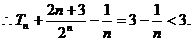
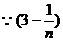 在N*是单调递增的, 在N*是单调递增的,
∴满足条件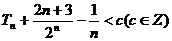 恒成立的最小整数值为 恒成立的最小整数值为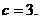 ……12分 ……12分 22.解:(Ⅰ)∵双曲线方程为  ∴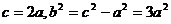 , , ∴双曲线方程为  ,又曲线C过点Q(2, ,又曲线C过点Q(2,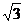 ), ), ∴ ∴双曲线方程为 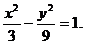 ………………5分 ………………5分 (Ⅱ)∵ ,∴M、B2、N三点共线 ,∴M、B2、N三点共线 ∵ , ∴ , ∴ (1)当直线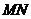 垂直x轴时,不合题意 垂直x轴时,不合题意 (2)当直线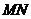 不垂直x轴时,由B1(0,3),B2(0,-3), 不垂直x轴时,由B1(0,3),B2(0,-3), 可设直线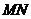 的方程为 的方程为 ,① ,① ∴直线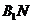 的方程为 的方程为 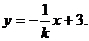 ② ② 由①,②知 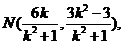 代入双曲线方程得 代入双曲线方程得  ,得 ,得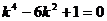 , ,
解得  , ∴ , ∴ , , 故直线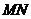 的方程为 的方程为  ………………12分 ………………12分
关闭

| |