12.直线与抛物线的交点
(1)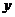 轴与抛物线
轴与抛物线 得交点为(0,
得交点为(0, 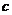 ).
).
(2)与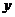 轴平行的直线
轴平行的直线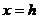 与抛物线
与抛物线 有且只有一个交点(
有且只有一个交点(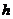 ,
,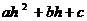 ).
).
(3)抛物线与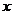 轴的交点
轴的交点
二次函数 的图像与
的图像与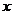 轴的两个交点的横坐标
轴的两个交点的横坐标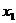 、
、 ,是对应一元二次方程
,是对应一元二次方程 的两个实数根.抛物线与
的两个实数根.抛物线与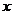 轴的交点情况可以由对应的一元二次方程的根的判别式判定:
轴的交点情况可以由对应的一元二次方程的根的判别式判定:
①有两个交点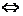
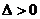
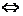 抛物线与
抛物线与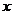 轴相交;
轴相交;
②有一个交点(顶点在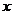 轴上)
轴上)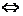
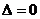
 抛物线与
抛物线与 轴相切;
轴相切;
③没有交点
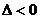
 抛物线与
抛物线与 轴相离.
轴相离.
(4)平行于 轴的直线与抛物线的交点
轴的直线与抛物线的交点
同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为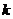 ,则横坐标是
,则横坐标是 的两个实数根.
的两个实数根.
 (5)一次函数
(5)一次函数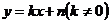 的图像
的图像 与二次函数
与二次函数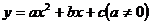 的图像
的图像 的交点,由方程组
的交点,由方程组 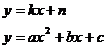 的解的数目来确定:①方程组有两组不同的解时
的解的数目来确定:①方程组有两组不同的解时
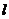 与
与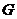 有两个交点; ②方程组只有一组解时
有两个交点; ②方程组只有一组解时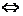
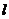 与
与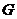 只有一个交点;③方程组无解时
只有一个交点;③方程组无解时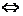
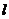 与
与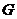 没有交点.
没有交点.
(6)抛物线与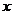 轴两交点之间的距离:若抛物线
轴两交点之间的距离:若抛物线 与
与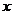 轴两交点为
轴两交点为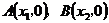 ,由于
,由于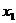 、
、 是方程
是方程 的两个根,故
的两个根,故
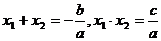
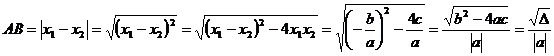
[能力训练]
- 答案

