到达O点前,把1、2和弹簧看作一个系统只有系统内的弹簧的弹性力作功,所以系统的机械能守恒,令v表示1和2到达O点时的速率,则有:

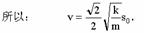
这就是分离时物体2的速率.

(2)分离后,在下一次相遇前,1以O点为平衡位置作简谐振动,振动的周期为:

从1和2分离时开始计时,即令该时刻t=0,则1通过O点的时刻为:

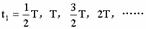
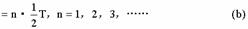
过O点后,2以匀速率v向右作直线运动.与B相碰时,由于碰撞是完全弹性

的,碰撞后2的速率不变,运动反向.

令x表示B与O点间的距离,则2返回O点的时刻为:

如2恰好在O点与1相遇,则:

t₂=t₁. (d)

将(b)、(c)两式代入(d),即得x应满足的条件为:

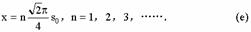
评分说明:全题14分.(1)4分,(2)10分.

(1)中,答出在O点分离的,给2分;列出机械能守恒方程并求出2的速率的,再给2分.

(2)中,知道和2分离后1作简谐振动,并写出振动周期公式(a)的,给2分;正确列出1经过O点的时刻t₁,即式(b)的,再给4分.对于t₁,只回答了n=1或n=2一次的,扣3分;只回答了n=1和n=2两次的,扣2分;只回答了n为奇数或为偶数一种情形的,扣2分.由于这一步考虑不全面,导致本题最后答案不全的,后面不重复扣分.

答出2与墙B碰撞后,速率不变,运动反向的(不要求证明),给1分,又正确求出2返回O点的时刻(c)的,再给1分.

正确列出1和2在O点相遇的条件,即(d)的,给1分;进一步求出距离x,即(e)的,再给1分.将(d)、(e)两步并作一步直接求出结果的,同样给2分.

本题中的单纯演算错误,可视其对物理过程或最后结果的影响程度,酌情扣分.