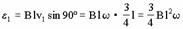
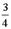=×0.05×0.08²×100伏特=0.024伏特. (a)

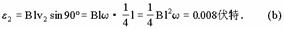
da段和bc段不切割磁力线,所以它们的电动势都是零.

(2)线框中的总电动势为:

ε=ε₁ +ε₂ 　=　 0.032伏特. (c)

线框中的感生电流为:

根据楞次定律或右手定则,可判断电流方向沿dcbad.

(3)解法一:

U_e-U_f是ebcf一段电路两端的电势差.它应等于eb段的路端电压U_eb,bc段两端的电势差U_bc与cf段的路端电压U_cf的代数和,即:

U_ef=U_eb+U_bc+U_cf.　　 (e)

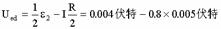
=0伏特, (f)

U_bc=-IR=-0.8×0.010伏特=-0.008伏特 (g)

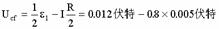
=0.008伏特,　　 (h)

所以:U_ef=U_eb+U_bc+U_cf

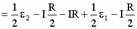
(i)

解法二:

闭合电路dcbad中的总电动势等于总电势降落.在edcf一段电路中,电动势等于总电动势的一半;电阻等于总电阻的一半,因而电势降落是总电势降落的一半,于是,在这段电路中,电势升正好等于电势降.由此可见,两端的电势差等于零.

评分说明:全题14分.(1)5分,(2)4分,(3)5分.

(1)中,正确求出ε₁和ε₂的,各给2分;答出da和bc段电动势都是零的,合给1分;单纯数字计算错误扣1分;ε₁和ε₂的答案数值正确而缺单位或单位错误的,无论出现一次或二次,只扣1分.

因把v=ωr的关系搞错而引起答案错误的,只扣1分.

(2)中,正确算出总电动势(c)的,给1分;进一步正确算出电流(d)的,再给2分;直接求出结果(d)的,同样给3分;电流方向正确的再给1分;数值错误和单位错误的扣分同(1)中规定.

(3)中,(e)、(f)、(g)和(h)各占1分;利用以上四式进一步正确算出结论(i)

的,再给1分;不分步计算,直接正确列出(i)式并算出结果的,同样给5分;单纯运算错误的,扣1分.

只有U_ef等于零的结论,而无任何推算过程、无任何论述或论述错误的,均不给分.结论正确但论述不够清楚的,酌情给分.