14.(城西中学)设F1、F2是双曲线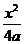 -
-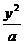 =1(a>0)的两个焦点
=1(a>0)的两个焦点
⑴若点P在双曲线上,且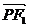 ·
·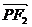 =0,|
=0,|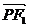 |·|
|·|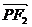 |=2,求双曲线的方程。
|=2,求双曲线的方程。
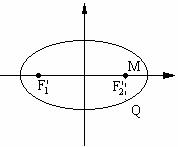
⑵设曲线C是以⑴中的双曲线的顶点为焦点,焦点为顶点的椭圆,若F1’、F2’分别是其左右 焦点,点Q是椭圆上任一点,M(2,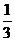 )是平面上一点,求|QM|+|QF1’|的最大值。
)是平面上一点,求|QM|+|QF1’|的最大值。
正确答案:⑴因为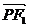 ·
·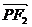 =0,∴
=0,∴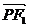 ⊥
⊥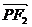 依题意
依题意
 |
|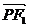 |2+|
|2+|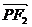 |2=|
|2=| |2 ①
|2 ①
|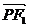 |+|
|+|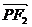 |=2 ②
|=2 ②
||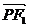 |-|
|-|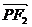 ||=4
||=4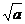 ③
③
①-③2:2|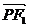 |·|
|·|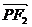 |=4a,将②代入得a=1,
|=4a,将②代入得a=1,
所以双曲线的方程为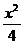 -y2=1
-y2=1
⑵由⑴及题意可得C的方程为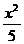 +y2=1,所以|QF1’|+|QF2’|=2
+y2=1,所以|QF1’|+|QF2’|=2
且F1’(-2,0),F2’(2,0),显然M点在椭圆内部。
所以|QM|+|QF1’|=|QM|+2 -|QF2’|≤2
-|QF2’|≤2 +|MF2’|
+|MF2’|
如图当|QM|-|QF2’|=|MF2’|时 |QM|-|QF2’|的值最大
所以|QM|+|QF1’|的最大值为2 +
+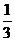
错因:第二问的转化出错。
- 答案

