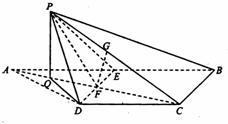
 ∵CD∥AB,
∵CD∥AB,
∴∠BAC=∠ACD.
又∵AD=CD,
∴∠DAC=∠ACD.
∴∠BAC=∠DAC.
即CA平分∠BAD.
∵△ADE是正三角形,
∴AC⊥DE.
即PF⊥DE,CF⊥DE.
∴DE⊥平面PCF.
∴DE⊥PC.
(2)过P作PO⊥AC于O,连结OD.
设AD=DC=CB=a,则AB=
∵DE⊥平面PCF,∴DE⊥PO.
∴PO⊥平面BCDE.
∴∠PDO即为直线PD与平面BCDE所成的角.
∵∠PFC是二面角P-DE-C的平面角,∴∠PFO=60°
- 答案
 ∵CD∥AB,
∵CD∥AB,
∴∠BAC=∠ACD.
又∵AD=CD,
∴∠DAC=∠ACD.
∴∠BAC=∠DAC.
即CA平分∠BAD.
∵△ADE是正三角形,
∴AC⊥DE.
即PF⊥DE,CF⊥DE.
∴DE⊥平面PCF.
∴DE⊥PC.
(2)过P作PO⊥AC于O,连结OD.
设AD=DC=CB=a,则AB=
∵DE⊥平面PCF,∴DE⊥PO.
∴PO⊥平面BCDE.
∴∠PDO即为直线PD与平面BCDE所成的角.
∵∠PFC是二面角P-DE-C的平面角,∴∠PFO=60°