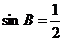
 ∵ , ∴ ∠B = 30°.
∵ , ∴ ∠B = 30°.
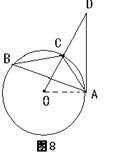
∵ ∠AOC = 2 ∠B , ∴ ∠AOC = 60°.
∵ ∠D = 30°, ∴ ∠OAD = 180°- ∠D - ∠AOD = 90°.
∴ AD是⊙O的切线.
(2) 解:∵ OA = OC ,∠AOC = 60°,
∴ △AOC是等边三角形 . ∴ OA = AC = 6 .
- 答案
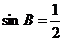
 ∵ , ∴ ∠B = 30°.
∵ , ∴ ∠B = 30°.
∵ ∠AOC = 2 ∠B , ∴ ∠AOC = 60°.
∵ ∠D = 30°, ∴ ∠OAD = 180°- ∠D - ∠AOD = 90°.
∴ AD是⊙O的切线.
(2) 解:∵ OA = OC ,∠AOC = 60°,
∴ △AOC是等边三角形 . ∴ OA = AC = 6 .