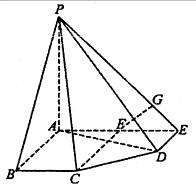
 (2)解法一:∵∠AED=90°,
(2)解法一:∵∠AED=90°,
∴AE⊥ED.
∵PA⊥平面ABCDE,
∴PA⊥ED.
∴ED⊥平面PAE.
过A作AG⊥PE于G,
过DE⊥AG,
∴AG⊥平面PDE.
过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角. 8分
- 答案
 (2)解法一:∵∠AED=90°,
(2)解法一:∵∠AED=90°,
∴AE⊥ED.
∵PA⊥平面ABCDE,
∴PA⊥ED.
∴ED⊥平面PAE.
过A作AG⊥PE于G,
过DE⊥AG,
∴AG⊥平面PDE.
过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角. 8分