19.(本小题满分12分)甲、乙两人各进行三次投篮,甲每次投中的概率为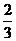 ,乙每次投中的概率为
,乙每次投中的概率为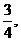 求:
求:
(1)甲恰好投中两次的概率;
(2)乙至少投中两次的概率;
(2)甲、乙两人共投中5次的概率.
- 答案
一、选择题
1.A 2.B 3.D 4.B 5.B 6.B 7.C 8.A 9.C
10.B 11.B 12.C
二、填空题
13. -3
14.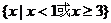
15.2
16.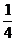
三、解答题
17.解:原不等式可化为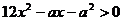
即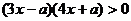
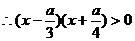 ………………………………6分
………………………………6分
当 …………8分
…………8分
当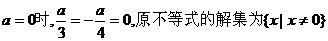 …………10分
…………10分
当 …………12分
…………12分
18.解: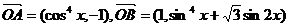
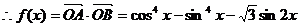
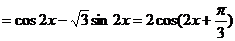 ………………6分
………………6分
(1)函数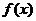 的最小正周期
的最小正周期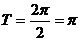 …………8分
…………8分
(2)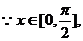
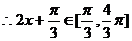
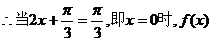 取得最大值.
取得最大值.
最大值为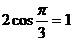 ………………12分
………………12分
19.解:
(1)甲恰好投中2次的概率为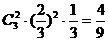 ………………3分
………………3分
(2)乙至少投中2次的概率为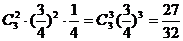 …………7分
…………7分
(3)设甲、乙两人共投中5次为事件A,甲恰好投中3次且乙恰投中2次为事件B1,甲恰投中2次且乙恰好投中3次为事件B2,则A=B1+B2,B1,B2为互斥事件.
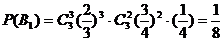 ………………9分
………………9分
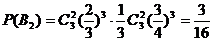 ………………11分
………………11分
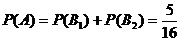
所以,甲、乙两人共投中5次的概率为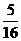 ………………12分
………………12分
20.解:
(1)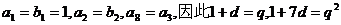
解得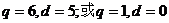 (舍去)…………5分
(舍去)…………5分
(2)假设存在a,b使得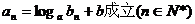
即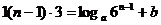
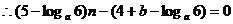 …………9分
…………9分
对于一切自然数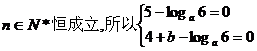
解得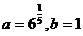 ……………………12分
……………………12分
21.解:
(1)设椭圆方程为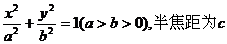 ,则
,则
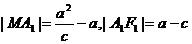 ,
,
由题意得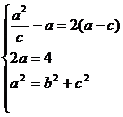 ………………4分
………………4分
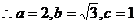
故椭圆方程为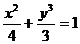 ………………6分
………………6分
(2)设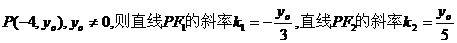 ,
,
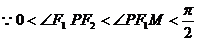
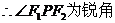
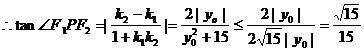 …………10分
…………10分
当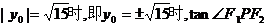 取到最大值,此时
取到最大值,此时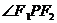 最大,故
最大,故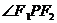 的最大为
的最大为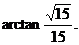 ………………12分
………………12分
22.解:由题设x1和x2是方程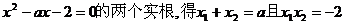 .
.
所以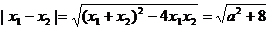
当 ………………3分
………………3分
由题意,不等式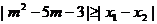 对于任意实数
对于任意实数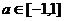 恒成立的m的解集等价于不等式
恒成立的m的解集等价于不等式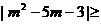 3的解集,由此不等式得
3的解集,由此不等式得
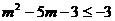 ①
①
或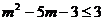 ②………………6分
②………………6分
不等式①的解为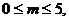 不等式②的解集为
不等式②的解集为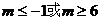
因此,当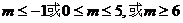 时,P是正确的…………7分
时,P是正确的…………7分
对函数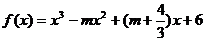 ,求导得
,求导得
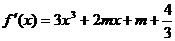
令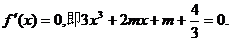
此一元二次方程的判别式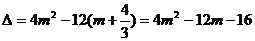
若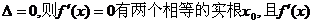 的符号如下
的符号如下
x
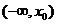
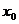
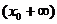
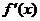
+
0
+
因此,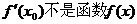 的根植.
的根植.
若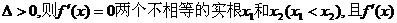 的符号如下
的符号如下
x
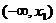
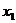
(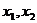 )
)
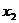
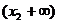
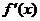
+
0
-
0
+
因此,函数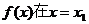 处取得极大值,在
处取得极大值,在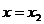 处取得极小值
处取得极小值
综上述,当且仅当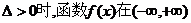 上有极值…………12分
上有极值…………12分
由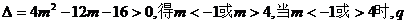 是正确的.
是正确的.
综上,使p正确且q正确时,实数m的取值范围是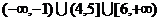
…………………………14分

