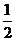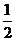∵ F、M分别是BE、BA的中点   ∴ FM∥EA, FM=EA

∵ EA、CD都垂直于平面ABC  ∴ CD∥EA∴ CD∥FM

又 DC=a,  ∴  FM=DC  ∴四边形FMCD是平行四边形

∴ FD∥MC

FD∥平面ABC

(2)       因M是AB的中点，△ABC是正三角形，所以CM⊥AB

又  CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF,

因F是BE的中点, EA=AB所以AF⊥EB.