g(x)∈M,∴存在区间[a,b]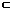 [1,+∞],满足g(a)=a,g(b)=b.
[1,+∞],满足g(a)=a,g(b)=b.
即方程g(x)=x在[1,+∞]内有两个不等实根.
[法一]:方程+t=x在[1,+∞]内有两个不等实根,等价于方程x-1=(x-t)2在[2t,+∞]内有两个不等实根.
即方程x2-(4t+4)x+4t2+4=0在[2t,+∞]内有两个不等实根.
- 答案
g(x)∈M,∴存在区间[a,b]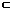 [1,+∞],满足g(a)=a,g(b)=b.
[1,+∞],满足g(a)=a,g(b)=b.
即方程g(x)=x在[1,+∞]内有两个不等实根.
[法一]:方程+t=x在[1,+∞]内有两个不等实根,等价于方程x-1=(x-t)2在[2t,+∞]内有两个不等实根.
即方程x2-(4t+4)x+4t2+4=0在[2t,+∞]内有两个不等实根.