12.某地2005年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
行业名称
计算机
机械
营销
物流
贸易
应聘人数
215 830
200 250
154 676
74 570
65 280
行业名称
计算机
营销
机械
建筑
化工
招聘人数
124 620
102 935
89 115
76 516
70 436
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是 ( )
A. 计算机行业好于化工行业. B. 建筑行业好于物流行业.
C. 机械行业最紧张. D. 营销行业比贸易行业紧张.
- 答案
一、选择题:
(1)D (2)B (3)C (4)B (5)B (6)A
(7)C (8)A (9)D (10)B (11)C (12)B
二、填空题:
(13)2
(14)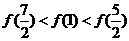 (15)200 (16)②③
(15)200 (16)②③
三、解答题
17.
(1) 故函数的定义域是(-1,1). ………… 2分
故函数的定义域是(-1,1). ………… 2分
(2)由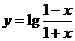 ,得
,得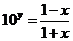 (
(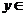 R),所以
R),所以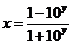 , …………… 5分
, …………… 5分
所求反函数为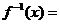
 (
( R).
………………… 7分
R).
………………… 7分
(3) 
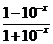 =
=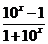 =-
=-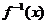 ,所以
,所以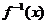 是奇函数.……… 12分
是奇函数.……… 12分
18. (1)设 ,则
,则 .
………………… 1分
.
………………… 1分
由题设可得 即
即 解得
解得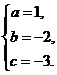 ………………… 5分
………………… 5分
所以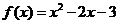 .
………………… 6分
.
………………… 6分
(2) 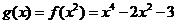 ,
,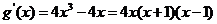 . …… 8分
. …… 8分
列表:


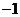


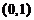


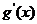
-

+

-

+


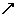

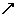
………………… 11分
由表可得:函数 的单调递增区间为
的单调递增区间为 ,
, ……………… 12分
……………… 12分
19.(1)证明:设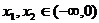 ,且
,且 ,
,
则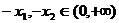 ,且
,且 .
………………… 2分
.
………………… 2分
∵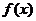 在
在 上是增函数,∴
上是增函数,∴ .
………………… 4分
.
………………… 4分
又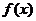 为奇函数,∴
为奇函数,∴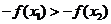 ,
,
∴ , 即
, 即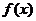 在
在 上也是增函数.
……………… 6分
上也是增函数.
……………… 6分
(2)∵函数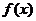 在
在 和
和 上是增函数,且
上是增函数,且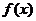 在R上是奇函数,
在R上是奇函数,
∴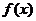 在
在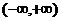 上是增函数.
…………………… 7分
上是增函数.
…………………… 7分
于是



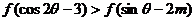

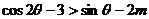

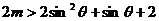

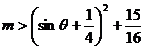 .
………… 10分
.
………… 10分
∵当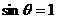 时,
时, 的最大值为
的最大值为 ,
,
∴当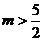 时,不等式恒成立.
……………… 12分
时,不等式恒成立.
……………… 12分
20. ∵AB=x, ∴AD=12-x. ………………1分
又 ,于是
,于是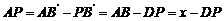 .
………………3分
.
………………3分
由勾股定理得 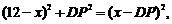 整理得
整理得 …………5分
…………5分
因此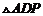 的面积
的面积 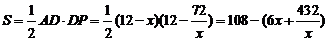 . ……7分
. ……7分
由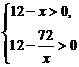 得
得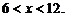 ………………8分
………………8分
∴
∴ .
………………10分
.
………………10分
当且仅当 时,即当
时,即当
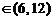 时,S有最大值
时,S有最大值 ……11分
……11分
答:当 时,
时,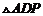 的面积有最大值
的面积有最大值 ………………12分
………………12分
21. (1) h (x) …………………5分
…………………5分
(2) 当x≠1时, h(x)=
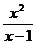 =x-1+
=x-1+ +2,
………………6分
+2,
………………6分
若 x > 1时, 则 h (x)≥4,其中等号当 x = 2时成立 ………………8分
若x<1时, 则h (x) ≤ 0,其中等号当 x = 0时成立 ………………10分
∴函数 h (x)的值域是 (-∞,0 ] ∪ { 1 } ∪ [ 4 ,+∞) ………………12分
22. (1)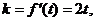
切线PQ的方程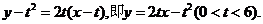 ………2分
………2分
(2)令y=0得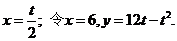 ………4分
………4分

由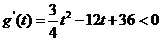 解得
解得 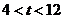 .
………6分
.
………6分
又0<t<6, ∴4<t<6, ………7分
g (t)在(m, n)上单调递减,故(m, n) ………8分
………8分
(3)当 在(0,4)上单调递增,
在(0,4)上单调递增,

∴P的横坐标的取值范围为 .
………14分
.
………14分

