20、(本小题满分16分)若有穷数列a1,a2,a3,……am(m∈N*)满足条件a1=am,a2=am―1,……,am=a1,我们称其为“对称数列”,例如1,2,5,2,1与数列8,4,2,2,4,8都是对称数列
(1)设{bn}是共有 7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11,请你依次写出{bn}的每一项;
(2)设{cn}是共有 49项的“对称数列”,其中c25,c26,……c49是首项为1,公比为q的等比数列,求{cn}各项和S;
- 答案
1、1
2、10
3、-49
4、70
5、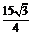
6、27 7、直角三角形 8、70 9、3 10、2
11、6 12、3<x<2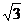 13、3
13、3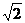 14、
14、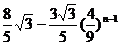
15解:(1)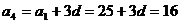 ………3分
………3分
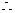
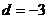
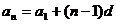 =28-3n
………7分
=28-3n
………7分
(2)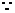
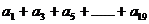

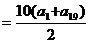 ………10分
………10分
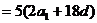
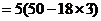 =
=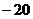 ………14分
………14分
16解:(1)由题意得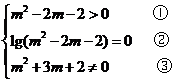 ……………………3分
……………………3分
由②得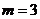 或
或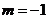 ,代入①③检验得
,代入①③检验得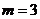 . ……………………5分
. ……………………5分
(2)由题意得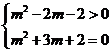 , ……………………7分
, ……………………7分
解得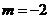 或
或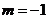 ,检验得
,检验得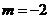 ,m=-1 ……………………10分
,m=-1 ……………………10分
(3)由题意得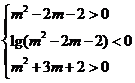 ……………………12分
……………………12分
解得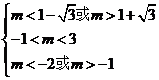
所以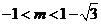 或
或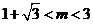 ……………………15分
……………………15分
17解、(I)由题意及正弦定理,得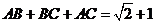 ①,
①,
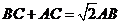 ②, ……………………4分
②, ……………………4分
两式相减,得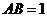 .
………………………6分
.
………………………6分
(II)由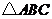 的面积
的面积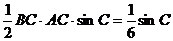 ,得
,得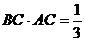 , …………8分
, …………8分
由余弦定理,得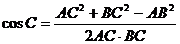 …………………10分
…………………10分
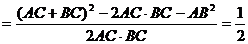 ………………12分
………………12分
又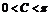 所以
所以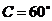 .
……………14分
.
……………14分
18 解:(1)A、B、C三点共线知存在实数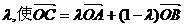 ………3分
………3分
即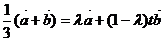 ,
,
则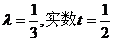 ………7分
………7分
(2)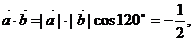 ………9分
………9分
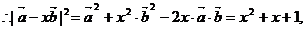 ………13分
………13分
当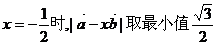 ………15分
………15分
19解:(I)m•n=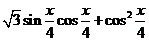 ┉┉┉┉2分
┉┉┉┉2分
=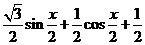 =
=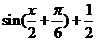 ┉┉┉┉┉4分
┉┉┉┉┉4分
∵m•n=1∴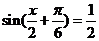 ┉┉┉┉┉┉5分
┉┉┉┉┉┉5分
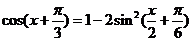 =
=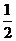 ┉┉┉┉┉┉7分
┉┉┉┉┉┉7分
(2)∵(
由正弦定理得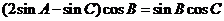 ┉┉┉┉┉┉9分
┉┉┉┉┉┉9分
∴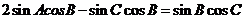
∴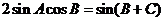
∵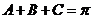
∴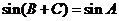 ,且
,且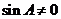
∴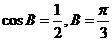 ┉┉┉┉┉┉12分
┉┉┉┉┉┉12分
∴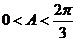
∴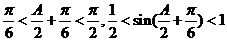 ┉┉┉┉┉┉14分
┉┉┉┉┉┉14分
又∵f(x)=m•n=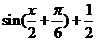 ,
,
∴f(A)=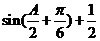
故函数f(A)的取值范围是(1,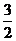 )
┉┉┉┉┉┉16分
)
┉┉┉┉┉┉16分
20.(1)由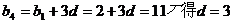 …………………………………2分
…………………………………2分
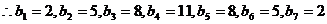 …………………5分
…………………5分
(2)q=1时,S=49
q≠1时,S=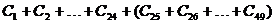
=2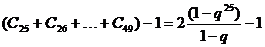 ………………9分
………………9分
(3)∵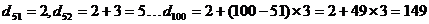
∴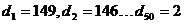
∴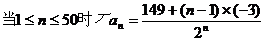
当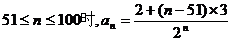 ……………………………………11分
……………………………………11分
∴当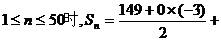
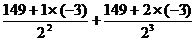
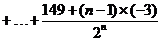
设T=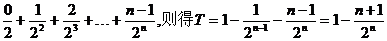
∴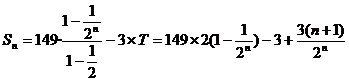
=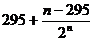 …………………………………………14分
…………………………………………14分
当51≤n≤100时,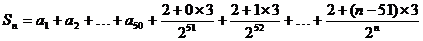
=295+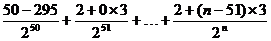
=295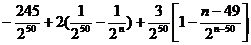
=295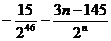 …………………………………16分
…………………………………16分

