14.AD
15.B
16.AC
17.C
18.D
19.BCD
20.A
第II卷(必做120分+选做32分,共152分)
[必做部分]
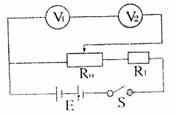
(2)如图(4分) (3)电压表V1的示数U1;电压表V2的示数U2(2分);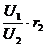 (1分) (1分) 22.0.15(0~2s时,水平力F>f即F=f=ma;2~6s,物体做匀速运动,F′=f,由v―t图线和P―t图线可知0~2s,P=F・v=(f+ma)v
①,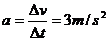 ②,2s时,v=6m/s,代入①式,P=30W,2~6s,物体做匀速运动, ②,2s时,v=6m/s,代入①式,P=30W,2~6s,物体做匀速运动,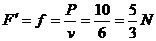 ③,0~6s,整个过程中 ③,0~6s,整个过程中 ④,解①②③④得μ=0.15。 ④,解①②③④得μ=0.15。 23.解: (1)设小球在M点的速率为v1,只加电场时对小球有M点
由牛顿第二定律得: (3分) (3分) 在水平轨道上,对小球由动能定理得: (3分) (3分) 联立解得E=32V/m (2分)
(2)设小球在N点的速率为v2,在N点,对小球由牛顿第二定律得: 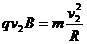 (3分) (3分)
从M点到N点,由机械能守恒定律得: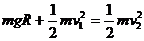 (3分) (3分) 联立解得: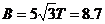 T (2分) T (2分) 说明:用其它解法的,只要科学合理,均可得分。 24.解:
(1)经时间t,杆ab的速率 v=at (1分) 此时,回路中的感应电流为 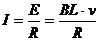 (1分) (1分)
对杆ab由牛顿第二定律得 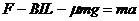 (2分) (2分)
由以上各式整理得: 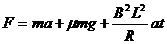 (1分) (1分)
在图线上取两点: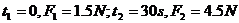 ,代入上式得 ,代入上式得 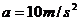 (1分) (1分)
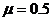 (1分) (1分)

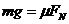 (2分)
(2分)
又FN=F安 (1分) F安=BIL
(1分) 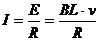 (1分) (1分)
 (1分)
(1分)
整理解得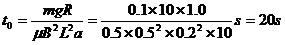 (1分) (1分)
|
关闭

| | | | | |