搜索
14．如图所示，木槽A质量为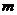
，置于水平桌面上，木槽上底面光滑，下底面与桌面间的动摩擦因数为
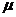，槽内放有两个滑块B和C（两滑块都看作质点），B、C的质量分别
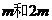，现用这两个滑块将很短的轻质弹簧压紧（两滑块与弹簧均不连接，弹簧长度忽略不计），此时B到木槽左端、C到木槽右端的距离均为L，弹簧的弹性势能为
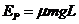。现同时释放B、C两滑块，并假定滑块与木槽的竖直内壁碰撞后不再分离，且碰撞时间极短求：
（1）滑块与槽壁第一次碰撞后的共同速度；
（2）滑块与槽壁第二次碰撞后的共同速度；
（3）整个运动过程中，木槽与桌面因摩擦产生的热量
- 答案
题号
1
2
3
4
5
6
7
8
9
10
答案
BCD
BD
BC
B
AB
C
B
D
C
D
11.⑴3m/s ⑵1400N
12.(1)设地球质量为M0，在地球表面，有一质量为m的物体，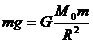
(2分)
设空间站质量为m′绕地球作匀速圆周运动时，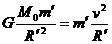
(2分)
联立解得，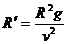
(2分)
(2)因为探测器对喷射气体做功的功率恒为P，而单位时间内喷气质量为m，故在t时
间内，据动能定理可求得喷出气体的速度为：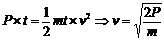
(2分)
另一方面探测器喷气过程中系统动量守恒，则：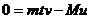
(2分)
又探测器的动能，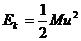
（２分）
联立解得：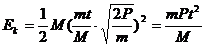
(１分)
13.
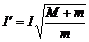（提示：第一次受到瞬时冲量I后，Q的动能是
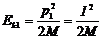，设细线长l，上摆过程Q的机械能守恒，Ek1=Mgl，因此
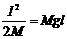①；第二次受到瞬时冲量I´后，Q的动量是I´，动能是
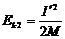，上摆到最高点P、Q刚好共速，该过程P、Q系统水平动量守恒，I´=(M+m)v，当时系统动能是
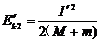，根据该过程系统机械能守恒，
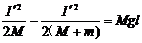②，由①②可得I´。）
14.（1）释放后弹簧弹开B、C两滑块的过程中，根据动量守恒定律和机械能守恒定律，有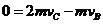
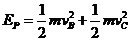（1分）
（1分）
解得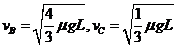
（2分）
式中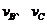
分别表示B、C两滑块离开弹簧时的速度大小。
滑块B经过时间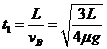
先与木槽A左侧壁碰撞，
设碰撞后达到的共同速度为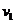
，则
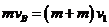（2分）
解得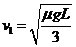
，方向水平向左
（2分）
（2）木槽A与B滑块相撞后，一起向左做匀减速运动，其加速度大小为
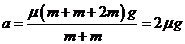（2分）
木槽A和滑块B相撞后速度减为0的时间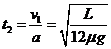
（1分）
在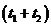
这段时同内．滑块C和木槽移动的距离之和为
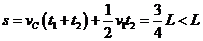，所以在C与A相撞前AB停止运动 （2分）
再经过一段时间．滑块C和木槽右侧壁碰撞。则
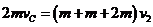（1分）
解得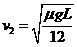
，方向水平向右
（2分）
（3）第一次碰撞后A与B的总动能全都转化为摩擦热
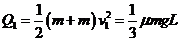（2分）
第二次碰撞后系统的总动能全都转化为摩擦热
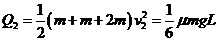（2分）
整个过程中木槽和桌面因摩擦而产生的热量为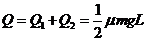
（2分
）
