4.0
- 答案
一.选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
C
A
D
C
B
A
D
D
A
二.13.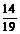 14.
14. 15.
15. 16.
16.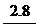 (万元)
(万元)
三.17.(I) 由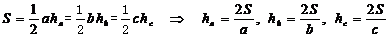
代入
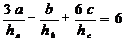 得:
得: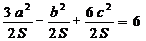
整理得: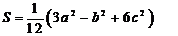 (5分)
(5分)
(II)由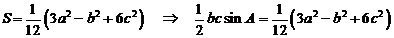
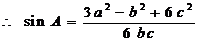 由余弦定理得:
由余弦定理得: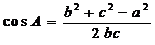
∴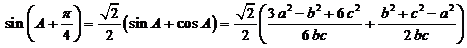
 -----------------------------
(9分)
-----------------------------
(9分)
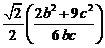
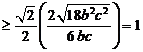
又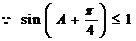
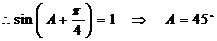 ------ (12分)
------ (12分)
18.(Ⅰ) 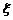 的分布列.
的分布列.
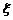
2
3
4
5
6
p
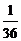
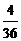
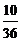
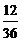

- --------- ------ (4分)
(Ⅱ)设掷出的两枚骰子的点数同是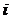 为事件
为事件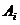
同掷出1的概率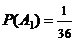 ,同掷出2的概率
,同掷出2的概率 ,同掷出3的概率
,同掷出3的概率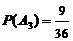
所以,掷出的两枚骰子的点数相同的概率为P=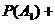
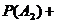
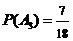 (8分)
(8分)
(Ⅲ)

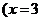 时)
时)
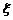
2
3
4
5
6
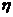
3
6
6
6
6
p
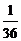
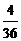
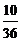
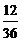

 =
=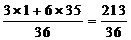
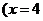 时)
时)
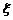
2
3
4
5
6
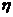
2
5
8
8
8
p
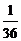
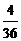
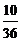
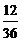

 =
=
 时)
时)
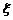
2
3
4
5
6
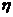
1
4
7
10
10
p
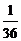
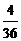
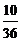
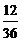

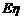 =
=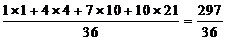
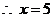 时,
时, 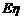 最大为
最大为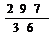 (12分)
(12分)
19.(Ⅰ)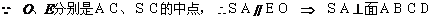


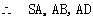 两两相互垂直, 连结
两两相互垂直, 连结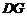 并延长交
并延长交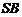 于F.
于F.
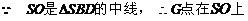
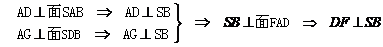
同理可得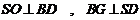
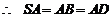
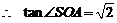 ------------ (6分)
------------ (6分)
(Ⅱ)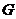 是
是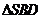 的重心
的重心
F是SB的中点
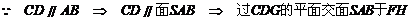
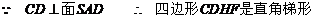
梯形的高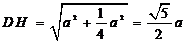
 --- (12分)
--- (12分)
【注】可以用空间向量的方法
20.设2,f (a1),
f (a2),
f (a3),
…,f (an), 2n+4的公差为d,则2n+4=2+(n+2-1)d  d=2,
d=2,
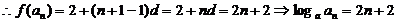
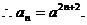 ……………………(4分)
……………………(4分)
(2)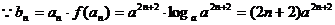 ,
,
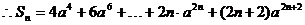
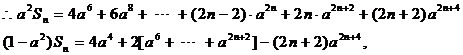
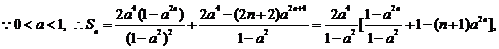 --------------------
(8分)
--------------------
(8分)
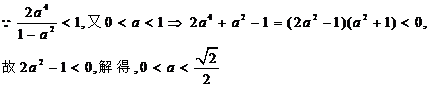
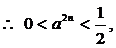
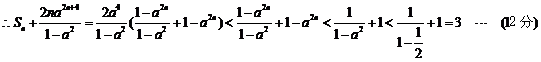
21.(Ⅰ)∵直线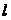 的斜率为1,抛物线
的斜率为1,抛物线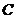 的焦点
的焦点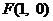
∴直线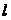 的方程为
的方程为
由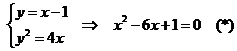
设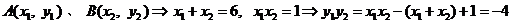
则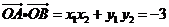
又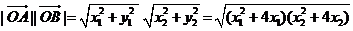
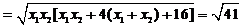

故 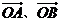 夹角的余弦值为
夹角的余弦值为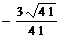 ----------------- (6分)
----------------- (6分)
(Ⅱ)由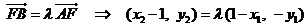
即得: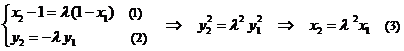
由 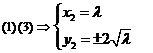
从而得直线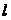 的方程为
的方程为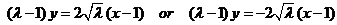
∴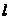 在
在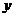 轴上截距为
轴上截距为 或
或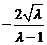
∵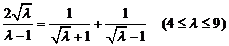 是
是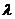 的减函数
的减函数
∴ 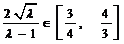 从而得
从而得
故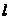 在
在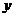 轴上截距的范围是
轴上截距的范围是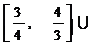
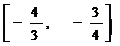 ------------ (12分)
------------ (12分)
22.(Ⅰ) 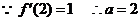
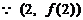 在直线
在直线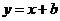 上,
上,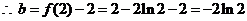
?????????????? (4分)
(Ⅱ)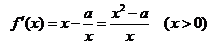
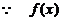 在
在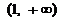 上是增函数,
上是增函数,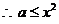 在
在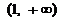 上恒成立
上恒成立
所以得 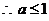 ??????????????? (8分)
??????????????? (8分)
(Ⅲ)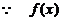 的定义域是
的定义域是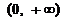 ,
,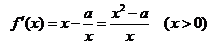
①当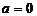 时,
时, 在
在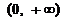 上单增,且
上单增,且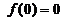 ,
,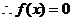 无解;
无解;
②当 时,
时,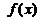 在
在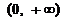 上是增函数,且
上是增函数,且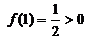 ,
,
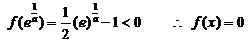 有唯一解;
有唯一解;
③当 时,
时,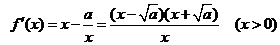
那么在 上
上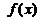 单减,在
单减,在 上
上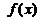 单增,
单增,
而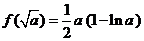
 时,
时, 无解;
无解;
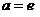 时,
时, 有唯一解
有唯一解 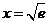 ;
;
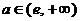 时,
时,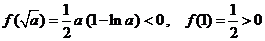
那么在 上,
上,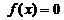 有唯一解
有唯一解
而在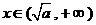 上,设
上,设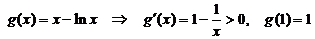

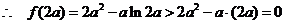
即得在 上,
上,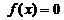 有唯一解.
有唯一解.
综合①②③得: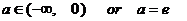 时,
时, 有唯一解;
有唯一解;
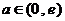
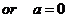 时,
时, 无解;
无解;
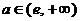 时,
时, 有且只有二解.
有且只有二解.
?????????????? (14分)

