(Ⅱ)设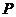 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线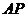 、
、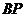 分别与椭圆相交于异于
分别与椭圆相交于异于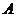 、
、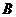 的点
的点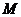 、
、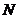 ,证明点
,证明点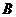 在以
在以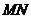 为直径的圆内.
为直径的圆内.
(此题不要求在答题卡上画图)
点评:本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力.
㈧定点和定值问题
(2007年全国卷II)已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且=λ(λ>0).过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明・为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
点评:本题考查抛物线及其切线问题,同时渗透利用均值定理求最值问题,综合性较强,对考生解题能力要求较多.
㈨解析几何应用问题
- 答案

