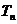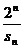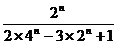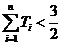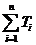（Ⅱ）解本问可先求出== , 欲证数列不等式，常规的方法有四种，即求和分析法，数学归纳法，利用数列单调性法，放缩法.对于本题来说，由于不等式左边是n的递增式，右边是常数，利用数列单调性法证左边式子的最大值小于是不可能的；同样由于n=k时比n=k+1左边式子要小，故不可利用数学归纳法求解；由于是在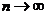时的极限（可求和证明），故不适于利用放缩法进行，最直接的方法是求和分析法，这也是证明数列不等式最常规的方法，也是最先考虑的方法. 由于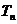是分式形式，可考虑裂项求和法，把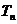变形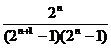为进而转化为(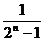-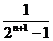) ，则问题迎刃而解.具体解法如下：