A.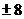 B.-8 C.8 D.
B.-8 C.8 D.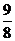
- 答案
一.选择题
CADAD CBCAD BB
二.填空题
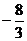 ;61; 4;
;61; 4; 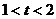
三.解答题
17. 解:(I)由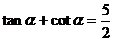 得
得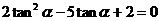 …………………………….2分
…………………………….2分
即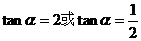 ,所以
,所以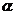 为第一、三象限角
为第一、三象限角
又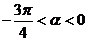 即
即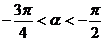 ,所以
,所以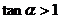 ,故
,故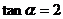 ……………..4分
……………..4分
(II)原式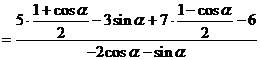 …………………………………6分
…………………………………6分
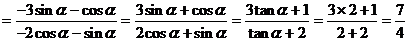 ……..10分
……..10分
18.解: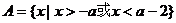 ……………..2分
……………..2分
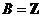 ……………..4分
……………..4分
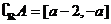 ,且该区间关于
,且该区间关于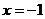 对称的. ……………..6分
对称的. ……………..6分
又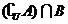 恰好有3个元素,所以
恰好有3个元素,所以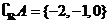 .
……………..8分
.
……………..8分
即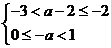 ,
……………..10分
,
……………..10分
解之得: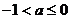 . ……………..12分
. ……………..12分
19. 解:(Ⅰ)∵ 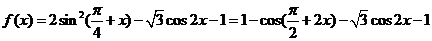
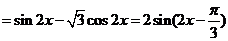 , ……………..2分
, ……………..2分
∴ 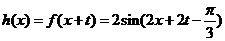 ,
,
∴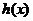 的图象的对称中心为
的图象的对称中心为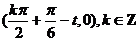 ,
……………..4分
,
……………..4分
又已知点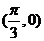 为
为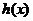 的图象的一个对称中心,∴
的图象的一个对称中心,∴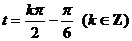 ,
,
而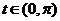 ,∴
,∴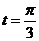 或
或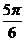 .
……………..6分
.
……………..6分
(Ⅱ)若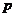 成立,即
成立,即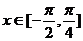 时,
时,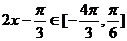 ,
,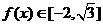 ,…8分
,…8分
由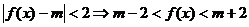 ,
……………..10分
,
……………..10分
∵ 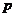 是
是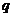 的充分条件,∴
的充分条件,∴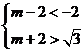 ,解得
,解得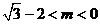 ,
,
即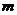 的取值范围是
的取值范围是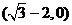 .
……………..12分
.
……………..12分
20.(1)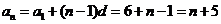 1分
1分
又当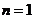 时,
时,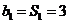 2分
2分
当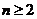 时,
时,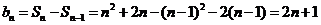
上式对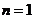 也成立,
也成立,
∴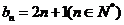 ,
,
总之,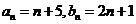 5分
5分
(2)将不等式变形并把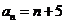 代入得:
代入得:
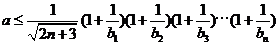 7分
7分
设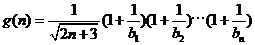
∴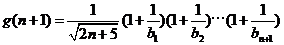
∴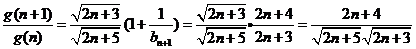
又∵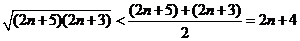
∴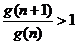 ,即
,即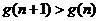 . 10分
. 10分
∴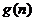 随
随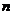 的增大而增大,
的增大而增大,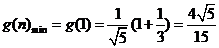 ,
,
∴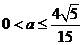 . 12分
. 12分
21. 解:(I)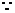
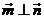 即
即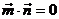
即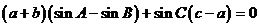 ………………………………………………..2分
………………………………………………..2分
由正弦定理得: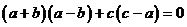
整理得: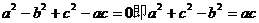 ………………………………………..4分
………………………………………..4分
由余弦定理得: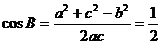
又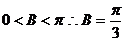 …………………………………………………………………………6分
…………………………………………………………………………6分
(II)由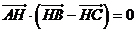 ,即
,即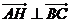
又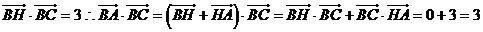 ……..8分
……..8分
另一方面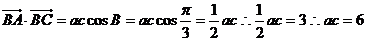 …………………...10分
…………………...10分
由余弦定理得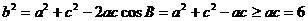
当且仅当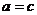 时取等号,所以
时取等号,所以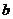 的最小值为
的最小值为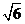 ……………………………………………12分
……………………………………………12分
22. 解:(I)由题意知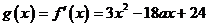 .
.
又对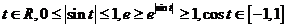 ,
,
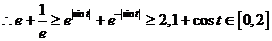 ,即
,即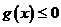 在
在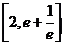 上恒成立,
上恒成立,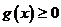 在
在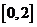 上恒成立。所以
上恒成立。所以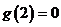 即
即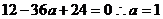 .………………………..........3分
.………………………..........3分
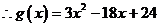 ,于是
,于是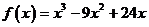
由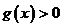 得
得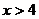 或
或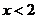 ,所以
,所以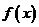 的递增区间为
的递增区间为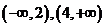 ………………….4分
………………….4分
(II)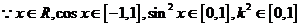 .
.
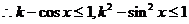 。又
。又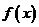 在
在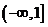 上是增函数,
上是增函数,
所以原不等式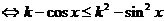
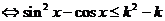 .
.
设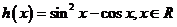 ,只需
,只需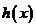 的最小值不小于
的最小值不小于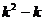 .………………………....6分
.………………………....6分
又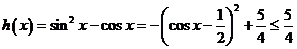 .
.
所以,当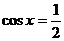 时取等号,即
时取等号,即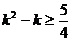 ,
,
解得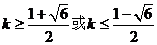 .
.
又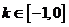 所以只需
所以只需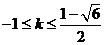 .
.
所以存在这样的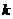 值使得不等式成立.………………………………………………………...8分
值使得不等式成立.………………………………………………………...8分
(III)由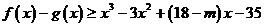 变形得
变形得
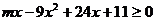 ,
,
令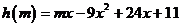 ,
,
要使对任意的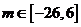 ,恒有
,恒有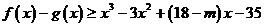 成立,
成立,
只需满足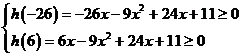 ,……………………………………...10分
,……………………………………...10分
解得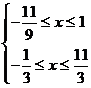 ,即
,即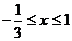 .……………………………………………………...12分
.……………………………………………………...12分
备选题:
设全集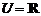 ,函数
,函数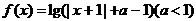 的定义域为A,集合
的定义域为A,集合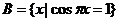 ,若
,若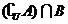 恰好有2个元素,求a的取值集合.
恰好有2个元素,求a的取值集合.
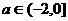
18.(本小题满分12分)
已知函数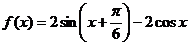 .
.
(Ⅰ)当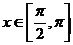 时,若
时,若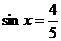 ,求函数
,求函数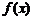 的值;
的值;
(Ⅱ)把函数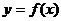 的图象按向量
的图象按向量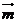 平移得到函数
平移得到函数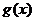 的图象,若函数
的图象,若函数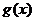 是偶函数,写出
是偶函数,写出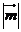 最小的向量
最小的向量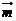 的坐标.
的坐标.
解:(Ⅰ)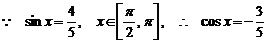 ,
,
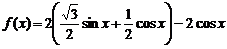
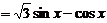
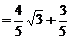 .
.
(Ⅱ)设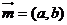 ,所以
,所以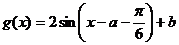 ,要使
,要使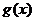 是偶函数,
是偶函数,
即要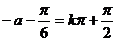 ,即
,即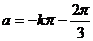 ,
,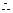
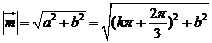 ,
,
当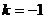 时,
时,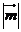 最小,此时
最小,此时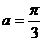 ,
,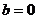 , 即向量
, 即向量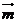 的坐标为
的坐标为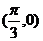
22.(本小题满分14分)
已知数列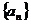 有
有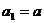 ,
,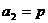 (常数
(常数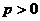 ),对任意的正整数
),对任意的正整数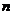 ,
,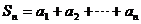 ,并有
,并有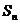 满足
满足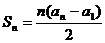 .
.
(Ⅰ)求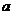 的值;
的值;
(Ⅱ)试确定数列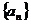 是否是等差数列,若是,求出其通项公式,若不是,说明理由;
是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(Ⅲ)对于数列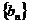 ,假如存在一个常数
,假如存在一个常数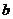 使得对任意的正整数
使得对任意的正整数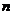 都有
都有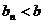 ,且
,且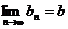 ,则称
,则称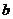 为数列
为数列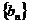 的“上渐近值”,令
的“上渐近值”,令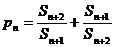 ,求数列
,求数列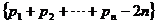 的“上渐近值”.
的“上渐近值”.
解:(Ⅰ)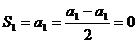 ,即
,即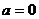
(Ⅱ)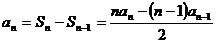
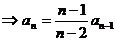
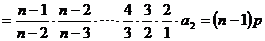
∴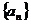 是一个以
是一个以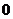 为首项,
为首项,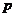 为公差的等差数列。
为公差的等差数列。
(Ⅲ)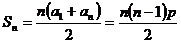
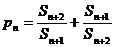
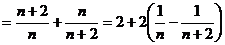
∴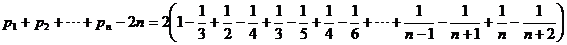
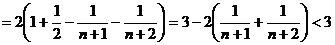
又∵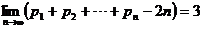 ,∴数列
,∴数列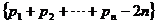 的“上渐近值”为
的“上渐近值”为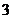 。
。

