所以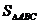 的最大值为
的最大值为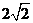 .
.
【点评】本题直接用“形”有一定的难度,若利用“数”运算,建立直角坐标系求解,则问题利于解决.这正好体现出“数形结合”思想,也进一步验证了
一个结论在一般情形下成立,在特殊情形下必成立。填空题只要结果,不要过程,所以当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时,可将填空题中的一般情形特殊化(将图形、图形的位置特殊化或给字母赋于特殊值等)再求解,这种解填空题的方法, 叫特殊化法。凡在一般情形下探求结论的填空题,都可用特例法。
- 答案
1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即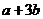 的最大值为2.
的最大值为2.
2. ∵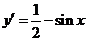 ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又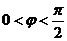 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若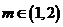 ,满足条件的
,满足条件的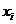 (
(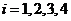 )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴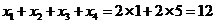 ;若
;若 ,满足条件的
,满足条件的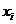 (
(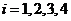 )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
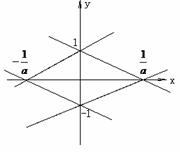
4. 不等式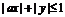 (
(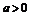 )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵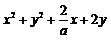
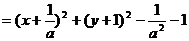 ,
,
当 ,点
,点 到点
到点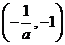 的距离最大,此时
的距离最大,此时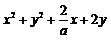 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点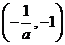 的距离最大,此时
的距离最大,此时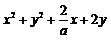 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵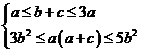 ,∴
,∴ ,
,
设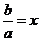 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为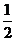 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点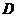 时,
时,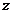 取得最小值.
取得最小值.
解方程组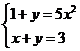 ,得
,得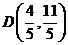 ,∴
,∴

