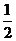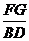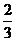解：依题意，可得EH∥BD，FG∥BD，故EH∥FG，由公理2可知，E、F、G、H共面，因为EH＝BD，＝，故EH≠FG，所以，EFGH是梯形，EF与GH必相交，设交点为M，因为点M在EF上，故点M在平面ACB上，同理，点M在平面ACD上，即点M是平面ACB与平面ACD的交点，而AC是这两个平面的交线，由公理3可知，点M一定在平面ACB与平面ACD的交线AC上。

选（D）。

点评：本题主要考查公理2和公理3的应用，证明共线问题。利用四个公理来证明共点、共线的问题是立体几何中的一个难点。