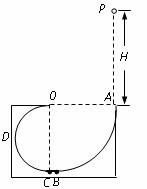
17．（18分）如图所示，ABCDO是处于竖直平面内的光滑轨道，AB是半径为R=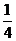15m的圆周轨道，CDO是直径为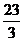15m的半圆轨道。AB轨道和CDO轨道通过极短的水平轨道（长度忽略不计）平滑连接。半径OA处于水平位置，直径OC处于竖直位置。一个小球P从A点的正上方高H处自由落下，从A点进入竖直平面内的轨道运动（小球经过A点时无机械能损失）。当小球通过CDO轨道最低点C时对轨道的压力等于其重力的倍，取g为10m/s2。

   （1）试求高度H的大小；

   （2）试讨论此球能否到达CDO轨道的最高点O，并说明理由；

   （3）求小球沿轨道运动后再次落回轨道上时的速度大小。

  • 答案

一、

题号

1

2

3

4

5

6

7

8

答案

B

D

C

A

B

C

B

C

二、

题号

9

10

11

12

答案

AC

B

BCD

AC

13．14.25.           14．① 0.40,  ②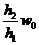,  ③ AC   ,  ④C

15．×1， ×10， 200。

16．解：

（1）设助跑距离为x，由运动学公式v2=2ax   -------------2分

    解得 x=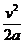=32.4m   ------------- 2分

（2）运动员过杆后做自由落体运动，设接触软垫时的速度为v'，由运动学公式有

   v'2=2gh2   -------------2分

  设软垫对运动员的作用力为F，由牛顿第二定律得

  F-mg =ma   -------------3分

  由运动学公式a=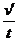  -------------2

  解得 F=1300 N   -------------2分

17．解：

（1）在C点对轨道的压力等于重力的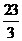倍，由牛顿第三定律得，在C点轨道对小球的支持力大小为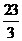mg--------1分。

    设小球过C点速度v1

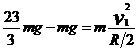 --------2分

    P到C过程，由机械能守恒：

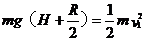 ---------2分

解得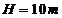：   ---------------1分www.ks5u

（2）设小球能到达O点，由P到O，机械能守恒，到O点的速度v2：

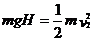
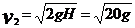                            --------2分 

     设小球能到达轨道的O点时的速度大小为v0，则

               mg =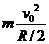       v0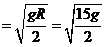     --------2分 

              v2 >v0   所以小球能够到达O点。    --------2分 

（3）小球在O点的速度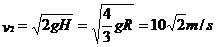

离开O点小球做平抛运动：

水平方向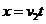： --------1分 

竖直方向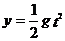：--------1分 

    且有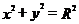：--------2分 

    解得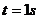：     再次落到轨道上的速度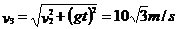--------2分 

18．解：

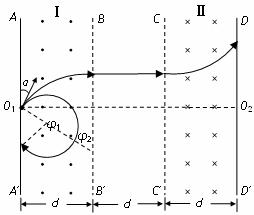
（1）若速度小于某一值时粒子不能从BB′ 离开区域Ⅰ，只能从AA′边离开区域Ⅰ。则无论粒子速度大小，在区域Ⅰ中运动的时间相同。轨迹如图所示（图中只画了一个粒子的轨迹）。则粒子在区域Ⅰ内做圆周运动的圆心角为φ1=300o，-------3分

由Bqv=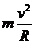 -------1分

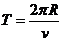    -------1分

得：粒子做圆周运动的周朔 T =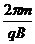 ---------2分

     由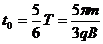   -------1分

      解得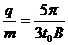： -------2分

（2）速度为v0时粒子在区域I内的运动时间为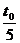，设轨迹所对圆心角为φ2。

     由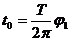 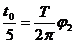       -------2分

     得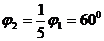： （3分）-------1分

所以其圆心在BB′上，穿出BB′ 时速度方向与BB′ 垂直，其轨迹如图所示，设轨道半径为R

由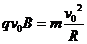   得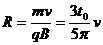：（2分）  -------2分

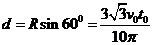     （2分）-------1分www.ks5u

（3）区域I、Ⅱ宽度相同，则粒子在区域I、Ⅱ中运动时间均为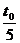，-------1分

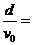
     穿过中间无磁场区域的时间为t′ = 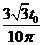 -------1分

    则粒子从O1到DD′所用的时间t=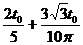 -------2分

关闭