9.圆心为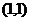 且与直线
且与直线 相切的圆的方程是_______________.
相切的圆的方程是_______________.
- 答案
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.D 2.B 3.D 4.A 5.C 6.D 7.C 8.A
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
9.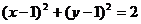 10.
10.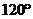 (或
(或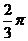 ) 11.
) 11.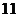
12.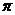 13.
13.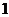 14.
14.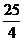
15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解: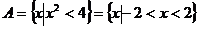 ,……………………………………………… 3分
,……………………………………………… 3分
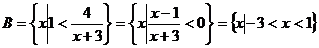 ,……………………… 3分
,……………………… 3分
(1) ;……………………………………………………. 2分
;……………………………………………………. 2分
(2)因为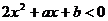 的解集为
的解集为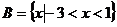 ,
,
所以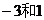 为
为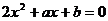 的两根,……………………………………… 2分
的两根,……………………………………… 2分
故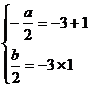 ,所以
,所以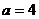 ,
,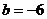 .……………………………………. 2分
.……………………………………. 2分
17.(本小题满分12分)
解: 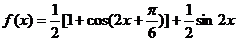 ………………………………………… 2分
………………………………………… 2分
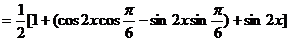
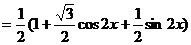 ………………………………………… 2分
………………………………………… 2分
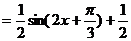 ……………………………………………………. 2分
……………………………………………………. 2分
(1) 的最大值为
的最大值为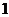 、最小值为
、最小值为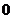 ;……………………………………………… 2分
;……………………………………………… 2分
(2) 单调增,故
单调增,故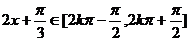 ,…………………………… 2分
,…………………………… 2分
即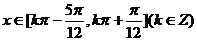 ,
,
从而 的单调增区间为
的单调增区间为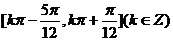 .…………………… 2分
.…………………… 2分
18.(本小题满分14分)
(1)证明: 底面
底面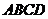 ,
,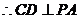
又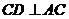 ,
,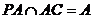 ,故
,故 面
面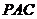
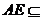 面
面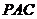 ,故
,故 ………………………………………………… 4分
………………………………………………… 4分
(2)证明: ,
, ,故
,故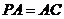
 是
是 的中点,故
的中点,故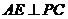
由(1)知 ,从而
,从而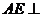 面
面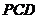 ,故
,故
易知 ,故
,故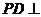 面
面 ……………………………………………… 5分
……………………………………………… 5分
(3)过点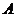 作
作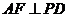 ,垂足为
,垂足为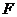 ,连结
,连结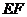 .
.
由(2)知,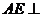 面
面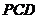 ,故
,故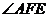 是二面角
是二面角 的一个平面角.
的一个平面角.
设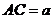 ,则
,则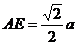 ,
,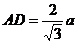 ,
,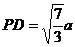
从而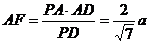 ,故
,故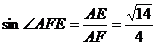 .……………… 5分
.……………… 5分
说明:如学生用向量法解题,则建立坐标系给2分,写出相关点的坐标给2分,第(1)问正确给2分,第(2)问正确给4分,第(3)问正确给4分。
19.(本小题满分14分)
解:(1)抛物线方程为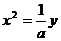 ……………………………………………………… 2分
……………………………………………………… 2分
故焦点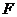 的坐标为
的坐标为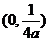 ………………………………………………………… 2分
………………………………………………………… 2分
(2)设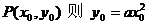
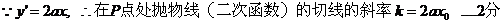

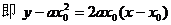

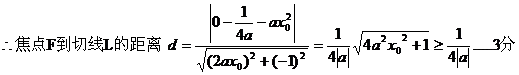
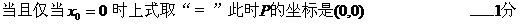
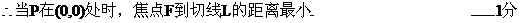
20.(本小题满分14分)
解:(1)当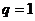 时,
时,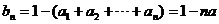 ,
,
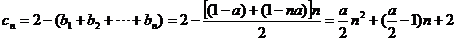
当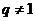 时,
时,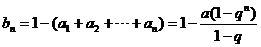
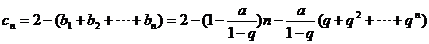
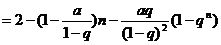
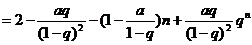
所以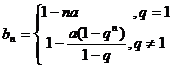
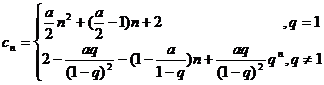 ;…………………… 4分
;…………………… 4分
(2)因为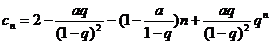 ,
,
所以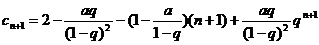

当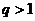 时,
时,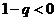 ,
,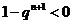
当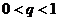 时,
时,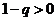 ,
,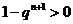
所以当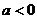 ,
,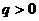 且
且 时,
时, ,即
,即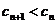 ;………… 5分
;………… 5分
(3)因为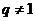 ,
,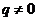 ,所以
,所以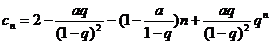 ,
,
因为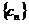 为等比数列,则
为等比数列,则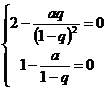 或
或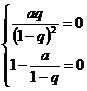 ,
,
所以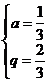 或
或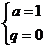 (舍去),所以
(舍去),所以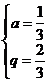 .………………………… 5分
.………………………… 5分
21.(本小题满分14分)
解:(1)由题意知, 的定义域为
的定义域为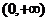 ,
,
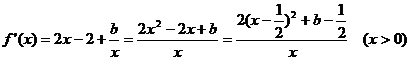 …… 1分
…… 1分
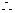 当
当 时,
时, 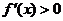 ,函数
,函数 在定义域
在定义域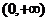 上单调递增. …… 2分
上单调递增. …… 2分
(2)①由(Ⅰ)得,当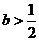 时,函数
时,函数 无极值点.
无极值点.
②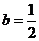 时,
时,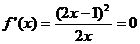 有两个相同的解
有两个相同的解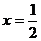 ,
,
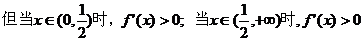 时,
时,
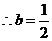 时,函数
时,函数 在
在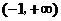 上无极值点.
…… 3分
上无极值点.
…… 3分
③当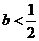 时,
时,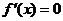 有两个不同解,
有两个不同解,
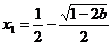
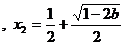
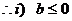 时,
时,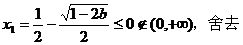 ,
,
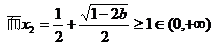 ,
,
此时 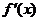 ,
, 随
随 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:

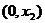
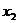
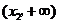
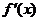
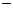
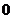
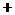

减
极小值
增
由此表可知: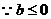 时,
时, 有惟一极小值点
有惟一极小值点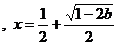 ,
…… 5分
,
…… 5分
ii) 当 时,0<
时,0<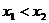 <1
<1
此时,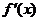 ,
, 随
随 的变化情况如下表:
的变化情况如下表:

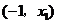
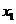
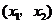
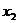
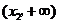
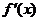
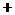
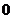
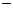
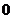

增
极大值
减
极小值
增
由此表可知: 时,
时, 有一个极大值
有一个极大值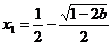 和一个极小值点
和一个极小值点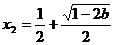 ;
……
7分
;
……
7分
综上所述:
当且仅当 时
时 有极值点;
…… 8分
有极值点;
…… 8分
当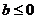 时,
时, 有惟一最小值点
有惟一最小值点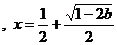 ;
;
当 时,
时, 有一个极大值点
有一个极大值点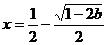 和一个极小值点
和一个极小值点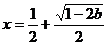
(3)由(2)可知当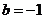 时,函数
时,函数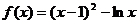 ,
,
此时 有惟一极小值点
有惟一极小值点
且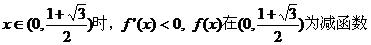 …… 9分
…… 9分
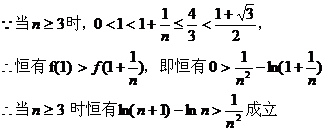 …… 11分
…… 11分
令函数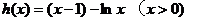
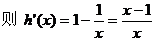 …… 12分
…… 12分
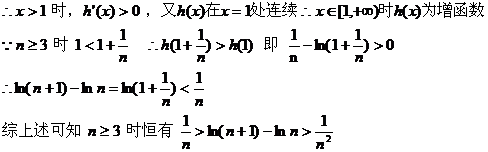 …… 14分
…… 14分

