19. 解法(一):(1)在△ABC中
解法(一):(1)在△ABC中
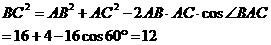
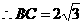
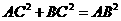
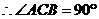 ,即
,即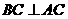 ,
,
由直三棱柱性质知:平面ACC1A1⊥平面ABC。
∴BC⊥平面ACC1A1
∴BC⊥A1C 又BC∥B1C1
∴B1C1⊥A1C ……………………………………………………………… 4分
(2)∵BC∥B1C1,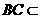 平面ABC,
平面ABC,
∴B1C1∥平面A1CB
∴B1点到平面A1CB的距离等于点C1到平面A1CB的距离。……………………6分
设点B1点到平面A1CB的距离为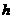 ,则
,则

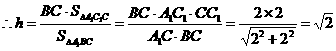 ………………………8分
………………………8分
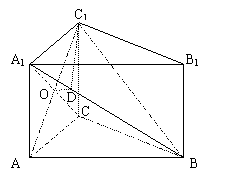
(3)连结AC1,交A1C于O,过O作OD⊥A1B于D,连结C1D
由(1)BC⊥平面ACC1A1得:平面BCA1⊥平面ACC1A1
由正方形ACC1A1知AC1⊥A1C
∴C1A⊥平面A1BC
∴OD是C1D在平面A1BC上的射影
∴C1D⊥A1B(三垂线定理)
∴∠ODC1是二面角C1-A1B-C的平面角。……………………………………10分
在△A1BC中,A1B=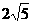 ,BC=
,BC=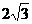 ,A1C=
,A1C=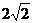 ,A1O=
,A1O=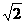 。
。
由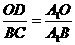 得:
得: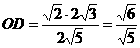
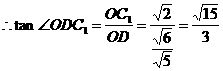
∴二面角C1-A1B-C的大小是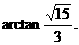 ……………………………………12分
……………………………………12分
解法(二)先证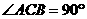 ,然后以C为原点,分别以CA、CB、CC1为
,然后以C为原点,分别以CA、CB、CC1为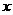 轴、
轴、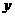 轴、
轴、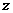 轴建立空间直角坐标系(略)
轴建立空间直角坐标系(略)
- 答案

