20.解:(1)过S作SH⊥BC于H,连 DH, ∵ 面BC ⊥面ABCD,∴SH⊥面ABCD ∴∠SDH为 SD和面ABCD所成的角。……3分
⊥面ABCD,∴SH⊥面ABCD ∴∠SDH为 SD和面ABCD所成的角。……3分
在正方形BB C
C C中,M,N分别为BB
C中,M,N分别为BB ,B
,B C
C 的中点,S位MN的中点,B
的中点,S位MN的中点,B C
C =4,
=4,
∴SH=3=CH,DH=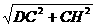 =
= ,在RTΔSHD中,tan∠SDH=
,在RTΔSHD中,tan∠SDH=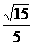 ……5分
……5分
延长B C
C 至E,使B
至E,使B C
C = C
= C E=4,连DE,ES, ∵C
E=4,连DE,ES, ∵C E平行且等于AD , ∴A C
E平行且等于AD , ∴A C ED为平行四边形。∴A C
ED为平行四边形。∴A C ∥ED,∴∠EDS为异面直线DS与A
C
∥ED,∴∠EDS为异面直线DS与A
C 所成的角。……8分
所成的角。……8分
在ΔDSE中,DS=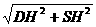 =2
=2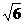 ,DE=
,DE=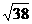 ,ES=5
,ES=5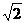 ,则cos∠EDS=
,则cos∠EDS=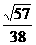 .
.
∴∠EDS=arccos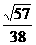 .即所求的角为arccos
.即所求的角为arccos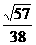 。……12分
。……12分
(附加题)连PD,过P作PF⊥面BB C
C C,垂足为F。过F作FG⊥MN于G,连结PG。
C,垂足为F。过F作FG⊥MN于G,连结PG。
由三垂线定理得PG⊥MN,d=PD.设d =PF,d
=PF,d =PG,在 RTΔPFG中,∵
=PG,在 RTΔPFG中,∵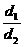 =
=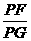 =sin∠PGF
=sin∠PGF
PG⊥MN,FG⊥MN, ∴∠PGF为二面角D-MN-C的平面角,设为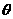 。又∵DC⊥MN, B
。又∵DC⊥MN, B C⊥MN,
C⊥MN,
∴d MN⊥面DSC. ∴∠DSC为
MN⊥面DSC. ∴∠DSC为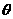 ,在RTΔDCS中,DC=
,在RTΔDCS中,DC=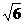 ,DS=2
,DS=2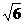 ,sin
,sin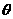 =
=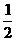 ………3分
………3分
∵d= d .∴
.∴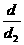 =
=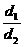 = sin
= sin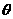 =
=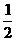 . 故
. 故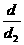 是一个定值
是一个定值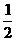 。………5分
。………5分
- 答案

