(15)(本小题12分)已知 |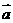 |=1,|
|=1,|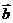 |=
|=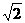 ,
,
(I)若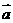 //
//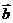 ,求
,求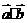 ; (II)若
; (II)若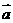 ,
,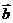 的夹角为135°,求 |
的夹角为135°,求 |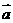 +
+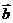 | .
| .
(16)(本小题12分) 袋中装有3个白球和4个黑球,现从袋中任取3个球,设ξ为所取出的3个球中白球的个数.
(I)求ξ的概率分布; (II)求Eξ.
(17)(本小题14分)
如图,已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为AA1、BB1的中点,求:
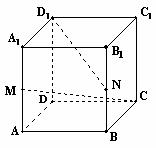 (I)CM与D1N所成角的余弦值;
(I)CM与D1N所成角的余弦值;
(II)异面直线CM与D1N的距离.
(18) (本小题14分)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM 上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米,
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
 (II)
若AN的长度不少于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最 小?并求出最小面积.
(II)
若AN的长度不少于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最 小?并求出最小面积.
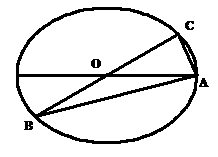
(19)(本小题14分) 如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且 ,|BC|=2|AC|.
,|BC|=2|AC|.
(I)建立适当的坐标系,求椭圆方程;
 (II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,
(II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,
证明:存在实数λ,使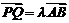 .
.
(20)(本小题14分) 已知数列{an}是首项为3,公比为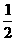 的等比数列,Sn是其前n项和.
的等比数列,Sn是其前n项和.
(Ⅰ)试用Sn表示Sn+1;
(Ⅱ)是否存在自然数c、k,使得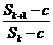 >3成立?证明你的论断.
>3成立?证明你的论断.
- 答案

