21. 设关于x的一元二次方程2x2-ax-2=0的两根的α、β(α<β),函数f(x)=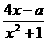
⑴求f(α)·f(β)的值;⑵证明f(x)是[α,β]的增函数;
(3)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小?
解:⑴ f(α)f(β)=-4
⑵设α≤x1<x2≤β,f(x1)-f(x2)=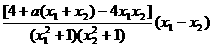 17. 已知函数
17. 已知函数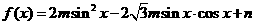 的定义域为
的定义域为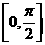 ,值域为
,值域为 .试求函数
.试求函数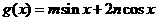 (
(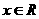 )的最小正周期和最值
)的最小正周期和最值
解: 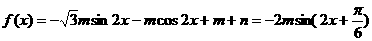
 ……2’
……2’
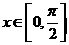
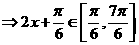
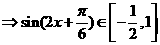 …………………………4’
…………………………4’
当 >0时,
>0时,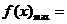
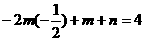 ,
,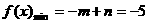
解得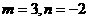 ,………………………………………………………………6’
,………………………………………………………………6’
从而,
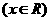 ,
,
T=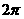 ,最大值为5,最小值为-5;………………………………………………8’
,最大值为5,最小值为-5;………………………………………………8’
当m<0时, 解得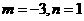 ,………………………………………………10’
,………………………………………………10’
从而, ,T=
,T=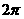 ,最大值为
,最大值为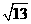 ,
,
最小值为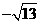 .……………………………………………………………………12
.……………………………………………………………………12
- 答案

