22.已知函数f(x)=-x3+ax2+b(a,b∈R)
(1)若函数y=f(x)图像上任意不同的两点连线斜率小于1,求证:-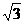 <a<
<a<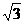
若x∈[0,1],函数y=f(x)上任一点切线斜率为k,讨论|k|≤1的充要条件
解:(1)设任意不同的两点P1(x1,y1),P2(x2,y2),且x1≠x2
则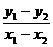 <1
(1分)
<1
(1分)
∴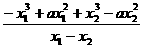 <1
<1
即-x12-x1x2-x22+a(x1+x2)<1
∴-x12+(a-x2)x1-x22+ax2-1<0 (3分)
∵x1∈R
∴Δ=(a-x2)2+4(-x22+ax2-1)<0
即-3x22+2ax2+a2-4<0
∴-3(x2-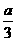 )2+
)2+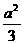 +a2-4<0
+a2-4<0
∴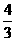 a2-4<0,∴-
a2-4<0,∴-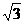 <a<
<a<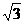 (6分)
(6分)
(2)当x∈[0,1]时,k=f′(x)=-3x2+2ax(7分)
由题意知:-1≤-3x2+2ax≤1,x∈[0,1]
即对于任意x∈[0,1],|f′(x)|≤1等价于|f′(0)|,|f′(1)|,
|f′(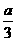 )|的值满足
)|的值满足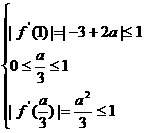
或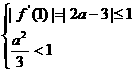 或
或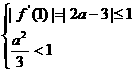 (11分)
(11分)
即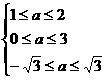 或
或 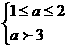 或
或 
∴1≤a≤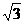
即|k|≤1的充要条件是1≤a≤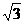
- 答案

