20.已知函数f(x)=x⁴－4x³+ax²－1在区间［0,1)上单调递增，在区间［1，2)上单调递减.

(Ⅰ)求a的值；

(Ⅱ)若点A(x₀,f(x₀))在函数f(x)的图象上，求证点A关于直线x=1的对称点B也在函数f(x)的图象上；

(Ⅲ)是否存在实数b，使得函数g(x)=bx²－1的图象与函数f(x)的图象恰有3个交点.若存在，请求出实数b的值；若不存在，试说明理由.

解：(Ⅰ)由函数f(x)=x⁴－4x³+ax²－1，在区间［0，1)上单调递增，在区间［1，2)上单调递减，

∴x=1时，f(x)取得极大值，∴f′(1)=0.　　　　　　 2分

f′(x)=4x³－12x²+2ax, ∴4－12+2a=0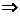a=4.　　　　　　　　　　 4分

(Ⅱ)点A(x₀,f(x₀))关于x=1的对称点B坐标为(2－x₀,f(x₀)),　　　　　 6分

f(2－x₀)=(2－x₀)⁴－4(2－x₀)³+4(2－x₀)²－1=(2－x₀)²［(2－x₀)－2］²－1

=x₀⁴－4x₀³+4x₀²－1=f(x₀).　　　　　　　　　　　　　　　　 8分

∴点A关于直线x=1的对称点B也在函数f(x)的图象上.　　　　　　　 9分

(Ⅲ)函数g(x)=bx²－1的图象与函数f(x)的图象恰有3个交点，等价于方程x⁴－4x³+4x²－1=bx²－1恰有3个不等实根，　　 　　　　　　　　　　 　 10分

x⁴－4x³+4x²－1=bx²－1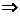x⁴－4x³+(4－b)x²=0.

∵x=0是其中一个根，

∴方程x²－4x+(4－b)=0有两个非0不等实根.　　　　　　　 　 12分

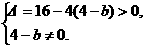∴∴b＞0且b≠4.　　　　　　　 　 14分