9.(I)令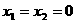 ,
,
依条件(3)可得f(0+0) ≥f(0)+f(0),即f(0) ≤0.
又由条件(1)得f(0) ≥0,则f(0)=0.
(Ⅱ)任取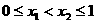 ,可知
,可知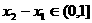 ,
,
则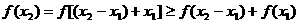 ,
,
即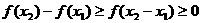 ,故
,故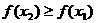
于是当0≤x≤1时,有f(x)≤f(1)=1
因此,当x=1时,f(x)有最大值为1,
(Ⅲ)证明:
研究①当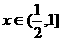 时,f(x) ≤1<2x
时,f(x) ≤1<2x
②当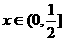 时,
时,
首先,f(2x) ≥f(x)+f(x)=2f(x),∴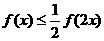 .
.
显然,当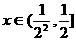 时,
时,
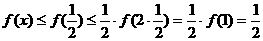 成立.
成立.
假设当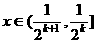 时,有
时,有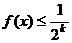 成立,其中k=1,2,…
成立,其中k=1,2,…
那么当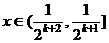 时,
时,

可知对于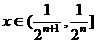 ,总有
,总有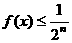 ,其中n=1,2,…
,其中n=1,2,…
而对于任意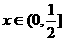 ,存在正整数n,使得
,存在正整数n,使得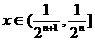 ,
,
此时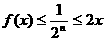 ,
,
③当x=0时,f(0)=0≤2x..
综上可知,满足条件的函数f(x),对x∈[0,1],总有f(x) ≤2x成立.
- 答案

