22.(12分)某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用为12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利? (2)若干年后,有两种处理方案:
方案一:年平均获利最大时,以26万元出售该渔船
方案二:总纯收入获利最大时,以8万元出售该渔船.问哪种方案合算.
解析:(1)由题意知,每年的费用以12为首项,4为公差的等差数列.
设纯收入与年数n的关系为f(n),则
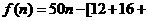 …
…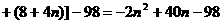 .
.
由题知获利即为f(n)>0,由 ,得
,得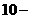
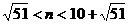 .
.
∴ 2.1<n<17.1.而n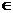 N,故n=3,4,5,…,17.∴ 当n=3时,即第3年开始获利.
N,故n=3,4,5,…,17.∴ 当n=3时,即第3年开始获利.
(2)方案一:年平均收入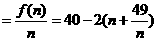 .
.
由于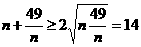 ,当且仅当n=7时取“=”号.
,当且仅当n=7时取“=”号.
∴ 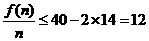 (万元).
(万元).
即第7年平均收益最大,总收益为12×7+26=110(万元).
方案二:f(n)=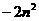 +40n-98=-2
+40n-98=-2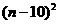 +102.
+102.
当n=10时,f(n)取最大值102,总收益为102+8=110(万元).
比较如上两种方案,总收益均为110万元,而方案一中n=7,故选方案一.
(23) (本小题满分14分)已知函数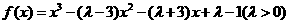 在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.
在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.
(1)求m0,n 0的值以及函数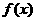 的解析式;
的解析式;
(2)已知等差数列{xn}的首项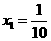 ,公差
,公差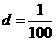 .又过点
.又过点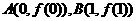 的直线方程为
的直线方程为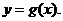 试问:在数列{xn}中,哪些项满足
试问:在数列{xn}中,哪些项满足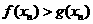 ?
?
(3)若对任意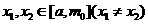 ,都有
,都有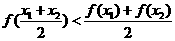 成立,求a的最小值.
成立,求a的最小值.
解(1)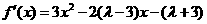 由题意可知
由题意可知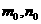 为方程
为方程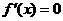 的两根
的两根
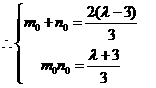 其中
其中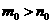
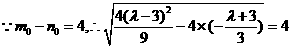
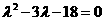 解得
解得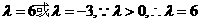
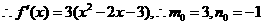
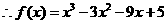
(2)由(1)得A(0,5),B(1,-6),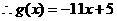 6/
6/
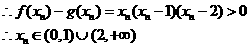
又由题得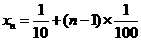 可解得
可解得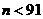 或
或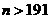
 当
当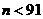 或
或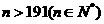 时,满足题意 (3)
时,满足题意 (3)
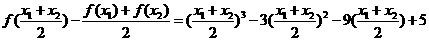
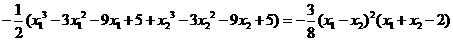 由题意,
由题意,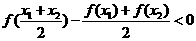 恒成立,即
恒成立,即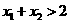 恒成立
恒成立
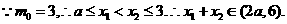
要使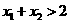 恒成立,只要
恒成立,只要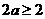 成立,即只要
成立,即只要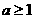 成立
成立
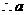 的最小值为1
的最小值为1
- 答案

