20.(本题12分)已知: 如图, 长方体AC1中, 棱AB=BC=3, 棱BB1=4, 连结B1C, 过点B作B1C的垂线交CC1于点E, 交B1C于点F.
(1) 求证: A1C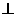 平面EBD;
平面EBD;
(2) 求点A到平面A1B1C的距离;
(3) 求ED与平面A1B1C所成角的大小.
解: (1)连结AC.在长方体AC1中, A1C在底面ABCD上的射影为AC, AC⊥BD,
∴AC1⊥BD. ……(2分)
在长方体AC1中, A1C在平面BB1C1C上的射影为B1C,B1C⊥BE, ∴A1C⊥BE. ……(3分)
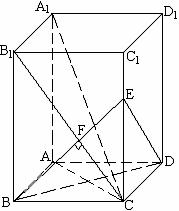 又BD
又BD BE=B, ∴A1C⊥平面EBD. ……(4分)
BE=B, ∴A1C⊥平面EBD. ……(4分)
(2) ∵BF⊥B1C, BF⊥AB1, B1C A1B1=B1,
A1B1=B1,
∴BF⊥平面A1B1C1, ……(5分)
又∵A1B1∥AB, A1B1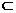 平面A1B1C,AB
平面A1B1C,AB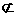 平面A1B1C,
平面A1B1C,
∴AB∥平面A1B1C, 点A到平面A1B1C的距离即为点
B到平面A1B1C距离, 也就是BF. ……(7分)
在△B1BC中, 易知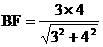
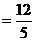 ,
,
点A到平面A1B1C的距离为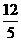 .……(8分)
.……(8分)
(3)连结A1D、FD. 由(2)知BE⊥平面A1B1C,
即BE⊥平面A1B1CD,
∴∠EDF为ED与平面A1B1C所成的角. ……(9分)
矩形B1BCC1中, 易求得B1F=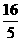 , CF=
, CF=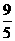 , EF=
, EF=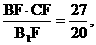 EC=
EC=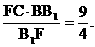
又在Rt△CDE中, 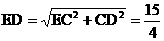 ,……(11分)
,……(11分)
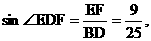 即ED与平面A1B1C所成角为
即ED与平面A1B1C所成角为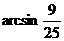 .……(12分)
.……(12分)
- 答案

