19.解:⑴ 令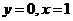 得
得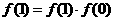 2分
2分
当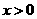 时,有
时,有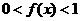 ,
,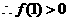
 4分
4分
当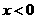 时,有
时,有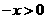 ,
,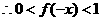 ,又
,又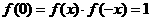
 7分
7分
⑵ 设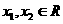 且
且
 9分
9分
又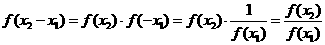 12分
12分
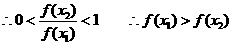

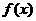 在
在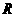 上单调递减.
14分
上单调递减.
14分
- 答案
19.解:⑴ 令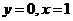 得
得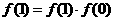 2分
2分
当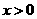 时,有
时,有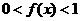 ,
,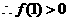
 4分
4分
当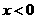 时,有
时,有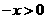 ,
,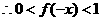 ,又
,又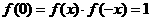
 7分
7分
⑵ 设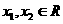 且
且
 9分
9分
又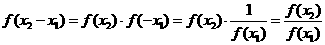 12分
12分
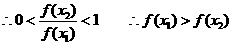

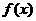 在
在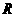 上单调递减.
14分
上单调递减.
14分