20、(本大题共16分)
[A类]设函数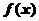 的定义域、值域均为R,
的定义域、值域均为R,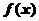 的反函数为
的反函数为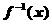 ,且对任意的实数
,且对任意的实数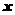 ,均有
,均有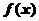 +
+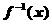
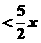 ,定义数列
,定义数列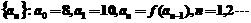
(1)求证: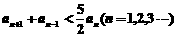
(2)设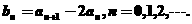 求证:
求证: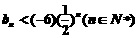
(3)是否存在常数A,B同时满足
1当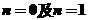 时,有
时,有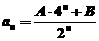 ,2
,2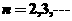 时,有
时,有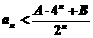 成立
成立
如果存在满足上述条件的A,B,则求出它们的值;若不存在,证明你的结论。
[B类]已知数列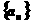 中,
中,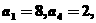 且满足
且满足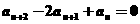 。
。
(1)求数列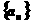 的通项公式
的通项公式
(2)设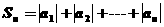 ,求
,求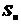
(3)设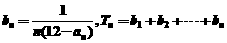 ,是否存在最大的整数
,是否存在最大的整数 ,使得对任意的
,使得对任意的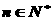 ,均有
,均有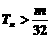 总成立,若存在,求出
总成立,若存在,求出 的值,若不存在,说明理由
的值,若不存在,说明理由
- 答案
20、(本大题共16分)
[A类]设函数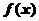 的定义域、值域均为R,
的定义域、值域均为R,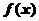 的反函数为
的反函数为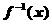 ,且对任意的实数
,且对任意的实数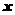 ,均有
,均有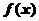 +
+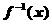
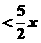 ,定义数列
,定义数列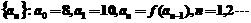
(1)求证: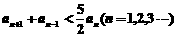
(2)设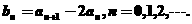 求证:
求证: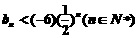
(3)是否存在常数A,B同时满足
1当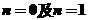 时,有
时,有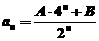 ,2
,2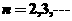 时,有
时,有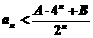 成立
成立
如果存在满足上述条件的A,B,则求出它们的值;若不存在,证明你的结论。
[B类]已知数列 中,
中,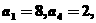 且满足
且满足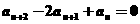 。
。
(1)求数列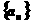 的通项公式
的通项公式
(2)设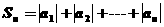 ,求
,求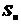
(3)设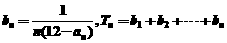 ,是否存在最大的整数
,是否存在最大的整数 ,使得对任意的
,使得对任意的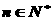 ,均有
,均有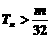 总成立,若存在,求出
总成立,若存在,求出 的值,若不存在,说明理由
的值,若不存在,说明理由