40.(山东卷)已知函数f(x)=A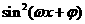(A>0,>0,0<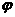<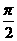函数，且y=f(x)的最大值为2，其图象相邻两对称轴间的距离为2，并过点(1，2).

(1)求;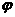

(2)计算f(1)+f(2)+… +f(2 008).

解：(I)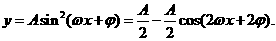

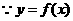的最大值为2，.

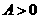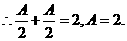
又其图象相邻两对称轴间的距离为2，，

.

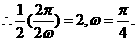
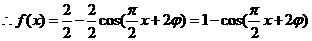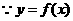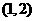过点，

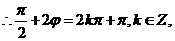
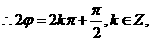
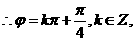
又.

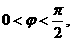
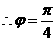(II)解法一：，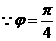

.

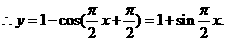
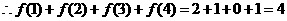又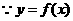的周期为4，，

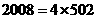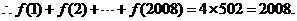
解法二：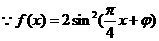

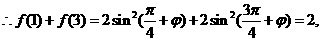
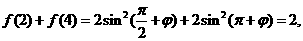
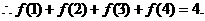
又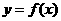的周期为4，，

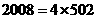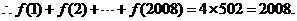
41(陕西卷)已知函数f(x)=sin(2x－)+2sin²(x－) (x∈R)

(Ⅰ)求函数f(x)的最小正周期　　 ;　 (2)求使函数f(x)取得最大值的x的集合.

解:(Ⅰ) f(x)=sin(2x－)+1－cos2(x－)

　　　　　 = 2[sin2(x－)－ cos2(x－)]+1

　　　　 =2sin[2(x－)－]+1

　　　　 = 2sin(2x－) +1　

∴ T==π

　 (Ⅱ)当f(x)取最大值时， sin(2x－)=1，有　 2x－ =2kπ+

即x=kπ+ 　 (k∈Z)　 ∴所求x的集合为{x∈R|x= kπ+ ，　 (k∈Z)}．