43.(天津卷)某射手进行射击训练,假设每次射击击中目标的概率为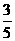 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);
(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);
(3)设随机变量 表示射手第3次击中目标时已射击的次数,求
表示射手第3次击中目标时已射击的次数,求 的分布列.
的分布列.
本小题考查互斥事件、相互独立事件的概率、离散型随机变量的分布列等基础知识,及分析和解决实际问题的能力.满分12分
解:(Ⅰ)记“射手射击1次,击中目标”为事件 ,则在3次射击中至少有两次连续击中目标的概率
,则在3次射击中至少有两次连续击中目标的概率
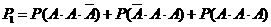
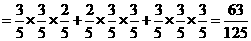
(Ⅱ)射手第3次击中目标时,恰好射击了4次的概率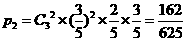
(Ⅲ)由题设,“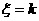 ”的概率为
”的概率为
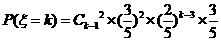
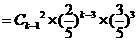 (
(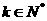 且
且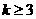 )
)
所以, 的分布列为:
的分布列为:
 |
3 |
4 |
… |
k |
… |
|
P |
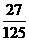 |
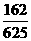 |
… |
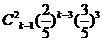 |
… |
- 答案

