22.(本小题满分12分)
已知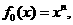
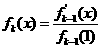 ,其中
,其中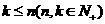 ,
,
设 ,
,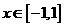 .
.
(I) 写出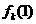 ;
;
(II) 证明:对任意的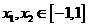 ,恒有
,恒有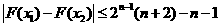 .
.
[解析](I)由已知推得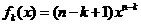 ,从而有
,从而有
(II) 证法1:当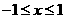 时,
时,
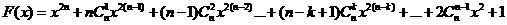
当x>0时, 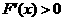 ,所以
,所以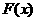 在[0,1]上为增函数
在[0,1]上为增函数
因函数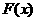 为偶函数所以
为偶函数所以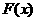 在[-1,0]上为减函数
在[-1,0]上为减函数
所以对任意的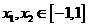
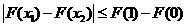
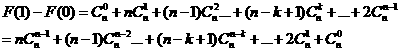
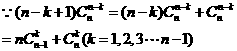
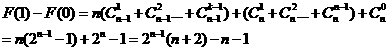
因此结论成立.
证法2: 当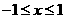 时,
时,
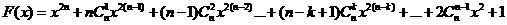
当x>0时, 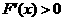 ,所以
,所以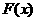 在[0,1]上为增函数
在[0,1]上为增函数
因函数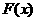 为偶函数所以
为偶函数所以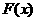 在[-1,0]上为减函数
在[-1,0]上为减函数
所以对任意的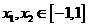
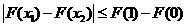
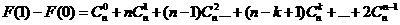
又因
所以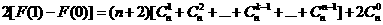
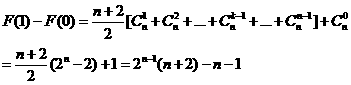
因此结论成立.
证法3: 当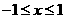 时,
时,
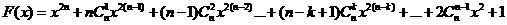
当x>0时, 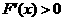 ,所以
,所以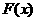 在[0,1]上为增函数
在[0,1]上为增函数
因函数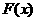 为偶函数所以
为偶函数所以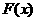 在[-1,0]上为减函数
在[-1,0]上为减函数
所以对任意的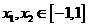
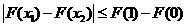
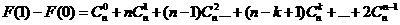
由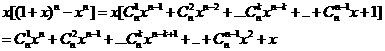
对上式两边求导得
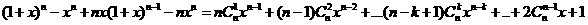
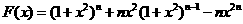
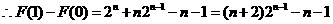
因此结论成立.
[点评]本小题考查导数的基本计算,函数的性质,绝对值不等式及组合数性质等基础知识,考查归纳推理能力以及综合运用数学知识分析问题和解决问题的能力.
- 答案

