(17)(本小题共12分)。
已知三棱锥P-ABC中,E、F分别是AC、AB的中点,
△ABC,△PEF都是正三角形,PF⊥AB.
(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P-AB-C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的球面上,
求△ABC的边长.
 ( 18 )(本小题共12分)
( 18 )(本小题共12分)
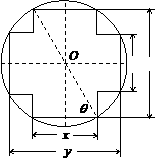
如图,在直径为1的圆 中,作一关于圆心对称、邻边互相
中,作一关于圆心对称、邻边互相
垂直的十字形,其中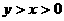 .
.
(Ⅰ)
将十字形的面积表示为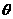 的函数;
的函数;
(Ⅱ)
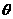 为何值时,十字形的面积最大?最大面积是多少?
为何值时,十字形的面积最大?最大面积是多少?
( 19 )(本小题共12分)
已知函数 .设数列
.设数列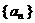 满足
满足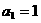 ,
,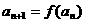 ,数列
,数列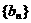 满足
满足
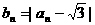 ,
,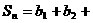 …
…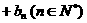 ,
,
(Ⅰ)用数学归纳法证明 ;(Ⅱ)证明
;(Ⅱ)证明 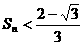 .
.
(20)(本小题满分12分)
某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
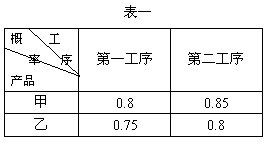 (Ⅰ)已知甲、乙两种产品每一道工序的
(Ⅰ)已知甲、乙两种产品每一道工序的
加工结果为A级的概率如表一所示,分别求生
产出的甲、乙产品为一等品的概率P甲、P乙;
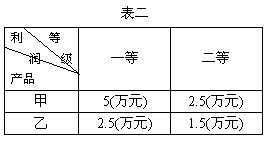 (Ⅱ)已知一件产品的利润如表二所示,用
(Ⅱ)已知一件产品的利润如表二所示,用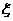 、
、
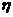 分别表示一件甲、乙产品的利润,在(Ⅰ)
分别表示一件甲、乙产品的利润,在(Ⅰ)
的条件下,求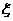 、
、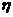 的分布列及
的分布列及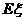 、
、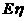 ;
;
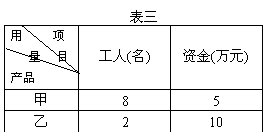 (Ⅲ)已知生产一件产品需用的工人数和资
(Ⅲ)已知生产一件产品需用的工人数和资
金如表三所示,该工厂有工人40名,可用资
金60万,设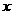 、
、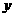 分别表示生产甲、乙产品
分别表示生产甲、乙产品
的数量,在(Ⅱ)的条件下,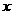 、
、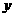 为何值时
为何值时
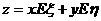 最大?最大值是多少?
最大?最大值是多少?
(解答时须给出图示)
 (21)(本小题满分14分)
(21)(本小题满分14分)
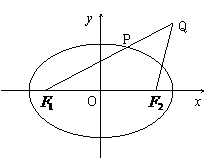
已知椭圆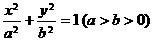 的左、右焦点分别是
的左、右焦点分别是
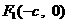 、
、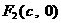 ,
,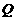 是椭圆外的动点,满足
是椭圆外的动点,满足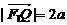 ,
,
点P是线段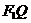 与该椭圆的交点,点T在线段
与该椭圆的交点,点T在线段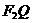 上,并且
上,并且
满足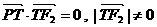 .
.
(Ⅰ)设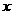 为点P的横坐标,证明
为点P的横坐标,证明 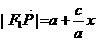 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△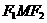 的面积
的面积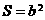 .若存在,求
.若存在,求
∠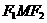 的正切值;若不存在,请说明理由.
的正切值;若不存在,请说明理由.
(22)(本小题满分12分)
函数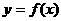 在区间
在区间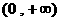 内可导,导函数
内可导,导函数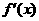 是减函数,且
是减函数,且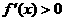 .设
.设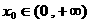 ,
,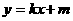 是曲线
是曲线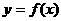 在点
在点 处的切线方程,并设函数
处的切线方程,并设函数
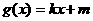 .
.
(Ⅰ)用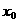 、
、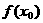 、
、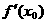 表示m;
表示m;
(Ⅱ)证明:当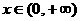 ,
,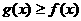 ;
;
(Ⅲ)若关于x的不等式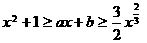 在
在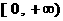 上恒成立,其中a、b为实数,求b的取值范围及a与b所满足的关系.
上恒成立,其中a、b为实数,求b的取值范围及a与b所满足的关系.
普通高等学校招生全国统一考试(辽宁卷)
- 答案

