(1)数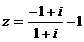 .在复平面内,z所对应的点在
(
)
.在复平面内,z所对应的点在
(
)
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
[答案]B
[解答]∵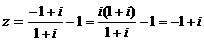
∴z所对应的点在第二象限.故选B.
[点拨]对于复数运算应先观察其特点再计算,会简化运算.
(2)极限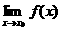 存在是函数
存在是函数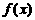 在点
在点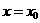 处连续的
( )
处连续的
( )
(A)充分而不必要的条件 (B)必要而不充分的条件
(C)充要条件 (D)既不充分也不必要的条件
[答案]B
[解答]∵极限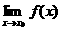 存在且
存在且 ,则函数
,则函数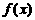 在点
在点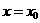 处连续的,
处连续的,
∴极限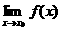 存在是函数
存在是函数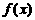 在点
在点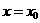 处连续的必要而不充分的条件,故选B.
处连续的必要而不充分的条件,故选B.
[点拨]准确理解函数连续性的概念及判断方法很重要.
(3)设袋中有80个红球,20个白球.若从袋中任取10个球,则其中恰有6个红球的概率为
(A)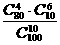 (B)
(B)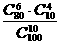 (C)
(C)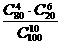 (D)
(D)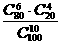
[答案]D
[解答]从袋中任取10个球有 种,其中恰有6个红球有
种,其中恰有6个红球有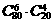 种,故选D.
种,故选D.
[点拨]分析如何完成取球任务,再利用组合计算.
(4)已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面.给出下列的四个命题:
①若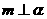 ,
,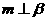 ,则
,则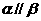 ;
;
②若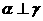 ,
,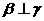 ,则
,则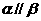 ;
;
③若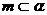 ,
,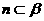 ,
,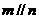 ,则
,则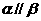 ;
;
④若m、n是异面直线,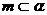 ,
,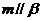 ,
,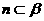 ,
,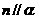 ,则
,则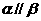 ,
,
其中真命题是
(A)①和② (B)①和③ (C)③和④ (D)①和④
[答案]D
[解答]因为垂直于同一条直线的两平面互相平行,所以①正确;因为垂直于同一平面的两平面不一定平行,所以②错误;因为当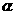 与
与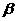 相交时,若m、n平行于两平面的交线,则
相交时,若m、n平行于两平面的交线,则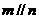 ,所以③错误;因为若m、n是异面直线,
,所以③错误;因为若m、n是异面直线,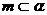 ,
,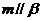 ,
,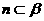 ,
,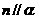 ,当且仅当
,当且仅当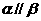 ,所以④正确.
,所以④正确.
[点拨]解立几推断题应联系具体图形以及相关定理解决.
(5)函数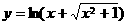 的反函数是
的反函数是
(A)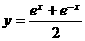 (B)
(B)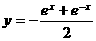 (C)
(C)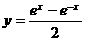 (D)
(D)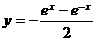
[答案]C
[解答]由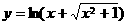 ,得
,得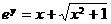 ,即
,即 ,
,
两边平方,化简得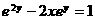 ,故
,故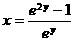 ,即
,即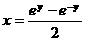 ,
,
∴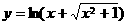 的反函数是
的反函数是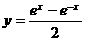 .
.
[点拨]求反函数设法解出x .
(6)若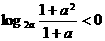 ,则a的取值范围是
,则a的取值范围是
(A)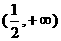 (B)
(B)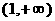 (C)
(C)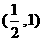 (D)
(D)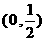
[答案]C
[解答]法一:代特殊值验证
法二:①当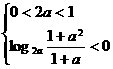 ,即
,即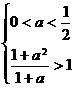 时,无解;
时,无解;
②当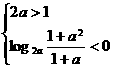 ,即
,即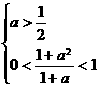 时,
时, ,故选C.
,故选C.
[点拨]解含参数对数不等式时,须注意分类讨论参数.
(7)在R上定义运算 :
: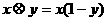 .若不等式
.若不等式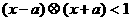 对任意实数x成立,则
对任意实数x成立,则
(A)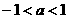 (B)
(B)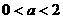 (C)
(C)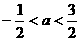 (D)
(D)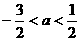
[答案]C
[解答]∵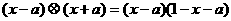 ,∴不等式
,∴不等式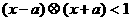 对任意实数x成立,则
对任意实数x成立,则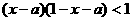 对任意实数x成立,即使
对任意实数x成立,即使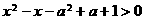 对任意实数x成立,所以
对任意实数x成立,所以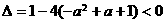 ,解得
,解得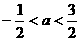 ,故选C.
,故选C.
[点拨]熟悉一元二次不等式恒成立与对应方程的判别式的关系.
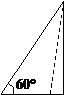
(8)若钝角三角形三内角的度数成等差数列,且最大边与最小边长的比值为m,则m的范围是
 (A)
(A) (B)
(B)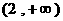 (C)
(C)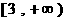 (D)
(D)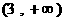
[答案]B
[解答]∵钝角三角形三内角的度数成等差数列,
∴其中一个角为60º,如图,直角三角形时,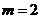 ,
,
所以钝角三角形时,有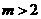 ,故选B.
,故选B.
[点拨]利用数形结合解题较快捷.
(9)若直线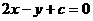 按向量
按向量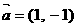 平移后与圆
平移后与圆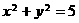 相切,则c的值为
相切,则c的值为
(A)8或-2 (B)6或-4 (C)4或-6 (D)2或-8
[答案]A
[解答]由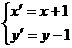 ,得
,得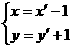 ,所以
,所以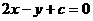 平移后,得
平移后,得 ,其与圆
,其与圆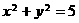 相切,即圆心到直线的距离为
相切,即圆心到直线的距离为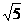 ,即
,即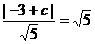 ,解得
,解得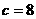 或
或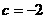 ,故选A.
,故选A.
[点拨]熟悉平移公式,直线与圆的位置关系应转化为圆心到直线的距离处理.
(10)已知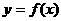 是定义在R上的单调函数,实数
是定义在R上的单调函数,实数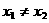 ,
,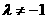 ,
,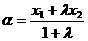 ,
,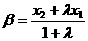 .若,则
.若,则
(A)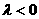 (B)
(B)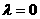 (C)
(C)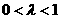 (D)
(D)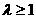
 [答案]A
[答案]A
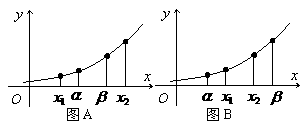
[解答]数形结合法:当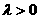 ,如图A所示,
,如图A所示,
有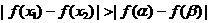 ,当
,当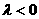 时,
时,
如图B所示,有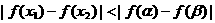 ,
,
故选A.
[点拨]数形结合解决定比分点问题.
(11)已知双曲线的中心在原点,离心率为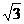 .若它的一条准线与抛物线
.若它的一条准线与抛物线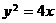 的准线重合,则
的准线重合,则
该双曲线与抛物线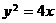 的交点到原点的距离是
的交点到原点的距离是
(A)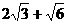 (B)
(B)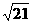 (C)
(C)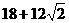 (D)21
(D)21
[答案]B
[解答]由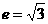 ,得
,得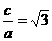 ,由一条准线与抛物线
,由一条准线与抛物线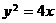 的准线重合,得准线为
的准线重合,得准线为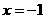 ,所以
,所以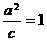 ,故
,故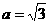 ,
,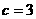 ,
,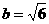 ,所以双曲线方程为
,所以双曲线方程为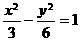 ,由
,由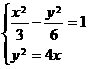 ,得交点为
,得交点为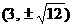 ,所以交点到原点的距离是
,所以交点到原点的距离是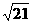 ,故选B.
,故选B.
[点拨]由已知条件发拨出a、b、c的取值,得到双曲线的方程.
(12)一给定函数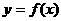 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意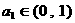 ,由关系式
,由关系式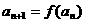
得到的数列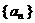 满足
满足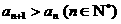 ,则该函数的图象是
,则该函数的图象是
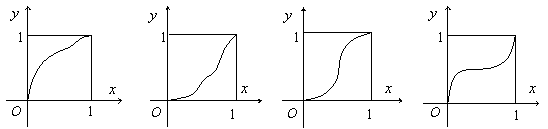
(A) (B) (C) (D)
[答案]A
[解答]由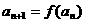 ,
,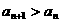 ,得
,得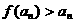 ,即
,即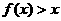 ,故选A .
,故选A .
[点拨]分析清楚函数值与自变量的关系,即可判断.
第Ⅱ卷 (非选择题 共90分)
- 答案

