21.解:(I)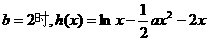 ,
,
则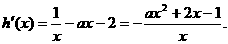
因为函数h(x)存在单调递减区间,所以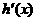 <0有解.
<0有解.
又因为x>0时,则ax2+2x-1>0有x>0的解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解;
则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0.
综上所述,a的取值范围为(-1,0)∪(0,+∞).
(II)证法一 设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为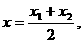
C1在点M处的切线斜率为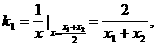
C2在点N处的切线斜率为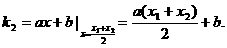
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2.
即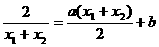 ,则
,则
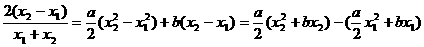
=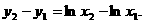
所以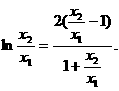 设
设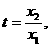 则
则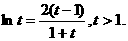 ①
①
令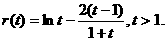 则
则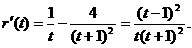
因为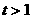 时,
时,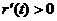 ,所以
,所以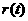 在
在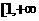 )上单调递增. 故
)上单调递增. 故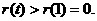
则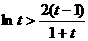 . 这与①矛盾,假设不成立.
. 这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
证法二:同证法一得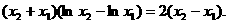
因为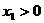 ,所以
,所以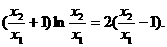
令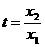 ,得
,得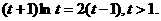 ②
②
令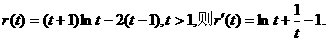
因为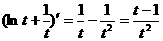 ,所以
,所以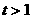 时,
时,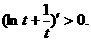
故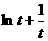 在[1,+
在[1,+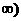 上单调递增.从而
上单调递增.从而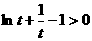 ,即
,即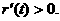
于是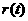 在[1,+
在[1,+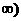 上单调递增.
上单调递增.
故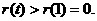 即
即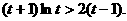 这与②矛盾,假设不成立.
这与②矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
- 答案

