20．解(I)从第n年初到第n+1年初，鱼群的繁殖量为ax_n，被捕捞量为bx_n，死亡量为

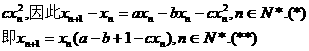
　 (II)若每年年初鱼群总量保持不变，则x_n恒等于x₁， n∈N*，从而由(*)式得

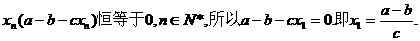
　　　　 因为x₁>0，所以a>b.

　　　　 猜测：当且仅当a>b，且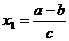时，每年年初鱼群的总量保持不变.

　 (Ⅲ)若b的值使得x_n>0，n∈N*

　　　　 由x_n+1=x_n(3－b－x_n), n∈N*, 知

　　　　 0<x_n<3－b, n∈N*, 特别地，有0<x₁<3－b. 即0<b<3－x₁.

　　　　 而x₁∈(0, 2)，所以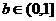

　　　　 由此猜测b的最大允许值是1.

　　　　 下证 当x₁∈(0, 2) ，b=1时，都有x_n∈(0, 2), n∈N*

　　　　 ①当n=1时，结论显然成立.

②假设当n=k时结论成立，即x_k∈(0, 2),

则当n=k+1时，x_k+1=x_k(2－x_k­)>0.

又因为x_k+1=x_k(2－x_k)=－(x_k－1)²+1≤1<2,

所以x_k+1∈(0, 2)，故当n=k+1时结论也成立.

由①、②可知，对于任意的n∈N*，都有x_n∈(0,2).

综上所述，为保证对任意x₁∈(0, 2), 都有x_n>0， n∈N*，则捕捞强度b的最大允许值是1.