19.(Ⅰ)证法一:因为A、B分别是直线l: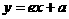 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是 .
.
所以点M的坐标是(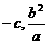 ). 由
). 由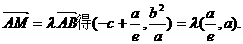
即
证法二:因为A、B分别是直线l: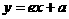 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是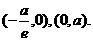 设M的坐标是
设M的坐标是
所以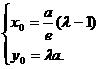 因为点M在椭圆上,所以
因为点M在椭圆上,所以 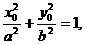
即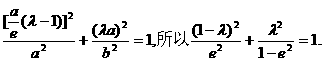
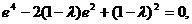 解得
解得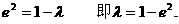
(Ⅱ)解法一:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即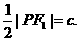
设点F1到l的距离为d,由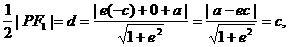
得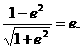 所以
所以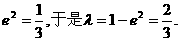
即当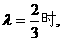 △PF1F2为等腰三角形.
△PF1F2为等腰三角形.
解法二:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,
设点P的坐标是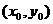 ,
,
则
由|PF1|=|F1F2|得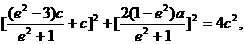
两边同时除以4a2,化简得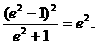 从而
从而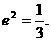
于是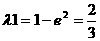 . 即当
. 即当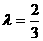 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.
- 答案

