22、已知函数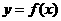 的定义域为
的定义域为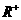 ,对任意
,对任意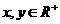 ,有恒等式
,有恒等式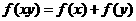 ;且当
;且当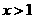 时,
时,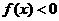 .
.
(1)求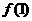 的值;
的值;
(2)求证:当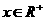 时,恒有
时,恒有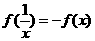 ;
;
(3)求证: 上为减函数;
上为减函数;
[以下(4)小题选理科的学生做;选文科的学生不做]
(4)由上一小题知: 上的减函数,因而
上的减函数,因而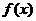 的反函数
的反函数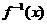 存在,试根据已知恒等式猜想
存在,试根据已知恒等式猜想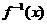 具有的性质,并给出证明.
具有的性质,并给出证明.
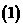 在已知等式中含
在已知等式中含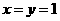 ,得
,得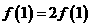 ,
,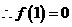 ----------理3分,文5分
----------理3分,文5分
 取
取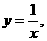 得
得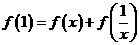
但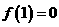 ,
,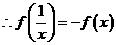 -------------------------------------------------理6分,文10分
-------------------------------------------------理6分,文10分
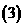 设
设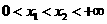 ,并令
,并令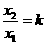 ,则
,则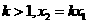
于是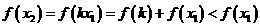
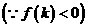
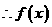 在
在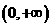 上为减函数----------------------------------------------------理12分,文18分
上为减函数----------------------------------------------------理12分,文18分
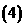 在
在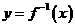 的定义域内,恒有
的定义域内,恒有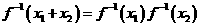 -----------理14分
-----------理14分
证明如下:设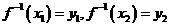 ,则
,则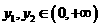
且 由题意设
由题意设
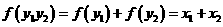
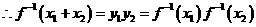 -------------------------------------------------理18分
-------------------------------------------------理18分
- 答案

