21、已知抛物线 (
(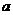 为实常数).
为实常数).
(1)求所有抛物线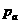 的公共点坐标;
的公共点坐标;
(2)当实数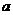 取遍一切实数时,求抛物线
取遍一切实数时,求抛物线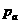 的焦点方程.
的焦点方程.
[理](3)是否存在一条以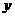 轴为对称轴,且过点
轴为对称轴,且过点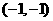 的开口向下的抛物线,使它与某个
的开口向下的抛物线,使它与某个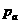 只有一个公共点?若存在,求出所有这样的
只有一个公共点?若存在,求出所有这样的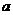 ;若不存在,说明理由.
;若不存在,说明理由.
[文](3)是否存在直线 (
( 为实常数),使它与所有的抛物线
为实常数),使它与所有的抛物线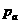 都有公共点?若存在,求出所有这样的直线;若不存在,说明理由.
都有公共点?若存在,求出所有这样的直线;若不存在,说明理由.
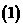 将抛物线
将抛物线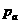 的方程该写成,
的方程该写成,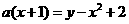
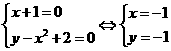
 所有的抛物线
所有的抛物线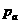 过完点
过完点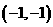 ,即
,即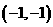 是所有抛物线
是所有抛物线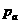 的公共点。-------------4分
的公共点。-------------4分

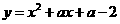
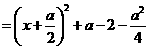 ,即
,即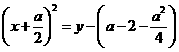
 抛物线
抛物线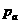 的顶点为
的顶点为 ,焦点坐标为
,焦点坐标为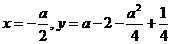
消去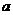 得焦点的轨迹方程:
得焦点的轨迹方程: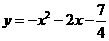 -----------------------------------------------------10分
-----------------------------------------------------10分
[理] 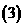 以
以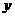 轴为对称轴,且过点
轴为对称轴,且过点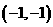 的开口向
的开口向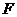 的抛物线可写成
的抛物线可写成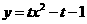
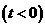 ------------------------------------------------------------------------------------------------------12分
------------------------------------------------------------------------------------------------------12分
设他与抛物线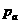 只有一个公共点,则方程
只有一个公共点,则方程
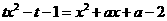 即
即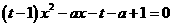
有两个相等的实根,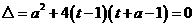
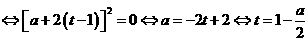 ----14分
----14分
由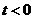
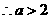 故当
故当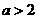 时,存在一条以
时,存在一条以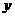 轴为对称轴且过点
轴为对称轴且过点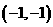 的开口向下的抛物线,
的开口向下的抛物线,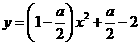 与
与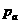 只有一个公共点------------------------------------------------16分
只有一个公共点------------------------------------------------16分
[文]  设
设 与一切
与一切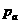 有公共点,则方程
有公共点,则方程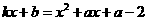 ,
,
即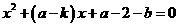 有实根
有实根
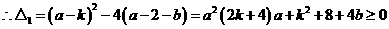
对一切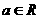 成立。--------------------------------------------------------------------------------------13分
成立。--------------------------------------------------------------------------------------13分
从而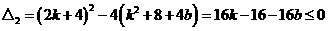
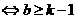
 当
当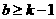 时直线
时直线 与一切
与一切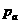 都有公共点。---------------------------------------16分
都有公共点。---------------------------------------16分
- 答案

